高中数学多面角及多面角的性质试题

已知函数的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（）和（）.
（I）求的解析式；
（II）用列表作图的方法画出函数y=f(x)在长度为一个周期的闭区间上的图象.

已知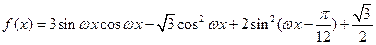（其中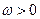）的最小正周期为。
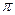求的单调递增区间；
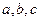在中，分别是角A，B，C的对边，已知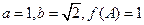，求角C。

函数的最小正周期是

A．

B．

C．

D．

（本小题满分12分）已知函数（其中，）．
（1）求函数的最小正周期；（2）若函数的图像关于直线对称，求的值．

下列关系式中正确的是                                                                         （   ）

A．	B．
C．	D．

（本小题满分10分）
已知向量，定义函数
，求函数的最小正周期、单调递增区间.

设a=（a₁，a₂）,b=（b₁,b₂）．定义一种向量积．已知，点P（x,y）在y=sinx的图象上运动,点Q在y=f（x）的图象上运动，且满足（其中O为坐标原点），则y=f（x）的最大值A及最小正周期T分别为（   ）

A．2,

B．2,4

C．

D．

(13分)已知向量设函数若的最小正周期为(1)求的值；(2)求的单调区间.

（本小题满分12分）已知函数
，且，又知函数（1）求的解析式；
（2）若将的图象向右平移个单位得到的图象，求的单调递增区间。

（本小题满分12分）已知 （1）求的最小正周期，并求其图象对称中心的坐标；  （2）当时，求函数的值域。

（本小题满分10分）
已知若，且的图象相邻的对称轴间的距离等于
（1）求的值；（2）在中，分别是角A，B，C的对边，，且，求的最小值。

（本小题满分13分）
已知，，其中，若函数，且的对称中心到对称轴的最近距离不小于（Ⅰ）求的取值范围；（Ⅱ）在中，分别是角的对边，且，当取最大值时，，求的面积.

 已知函数
（1）若函数；
（2）设，若p是q的充分条件，求实数m的取值范围.

（本小题满分13分）设函数．（1）求的最小正周期（2）若函数与的图像关于直线对称，求当时的最大值．

（本小题满分13分）设函数．（1）求的最小正周期（2）若函数与的图像关于直线对称，求当时的最大值．