湖北省八校高三第二次联考数学(理)
为得到函数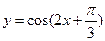 的图象,只需将函数
的图象,只需将函数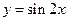 的图象 ( )
的图象 ( )
A.向左平移 个长度单位 个长度单位 |
B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 |
D.向右平移 个长度单位 个长度单位 |
如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,则以下命题中,错误的命题是 
A.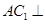 平面A1BD 平面A1BD |
B.H是 的垂心 的垂心 |
C. |
| D.直线AH和BB1所成角为45° |
甲、乙、丙、丁、戌5人站成一排,要求甲、乙均不与丙相邻,则不同的排法种数为( )
| A.72种 | B.54种 | C.36种 | D.24种 |
已知椭圆方程为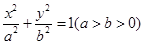 ,O为原点,F为右焦点,点M是椭圆右准线
,O为原点,F为右焦点,点M是椭圆右准线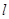 上(除去与
上(除去与 轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
A. |
B.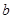 |
C.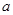 |
D.不确定 |
填空题已知数列
 为等差数列,
为等差数列, 为其前
为其前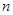 项和
项和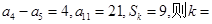
函数
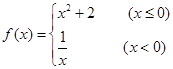 的反函数为
的反函数为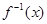 ,则
,则 。
。已知球O的表面上四点A、B、C、D,
 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC=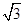 ,则球O的体积等于 。
,则球O的体积等于 。某校在2010年的“八校第一次联考”中有1000人参加考试,数学考试的成绩
 (
(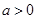 ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。有一种数学推理游戏,游戏规则如下:

①在9×9的九宫格子中,分成9个3×3的小九格,用1到9这9个数填满整个格子;
②每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每 行每列及每个小九宫格里只能出现一次,既不能重复也不能少,那么A处应填入的数字为 ;B处应填入的数字为 。
2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为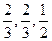 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。求A能够入选的概率;
规定:按人选人数得训练经费(每人选1人,则相应的训练基地得到3000元的训练经费),求该基地得到训练经费的分布列与数学期望。
如图,在直角梯形ABCD中,AD//BC, ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。判断直线AD与BC是否共面,并证明你的结论;
当直线AC与平面EFCD所成角为多少时,二面角A—DC—E的大小是60°。

某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这一产品期间第 天的利润
天的利润 (单位:万元,
(单位:万元,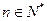 ),记第
),记第 天的利润率
天的利润率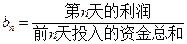 ,例如
,例如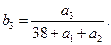
求
 的值;
的值;求第
 天的利润率
天的利润率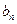 ;
;该商店在经销此纪品期间,哪一天的利润率最大?并求该天的利润率。
定长为3的线段AB两端点A、B分别在 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且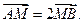
(1)求点M的轨迹C的方程;
(2)设过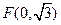 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
 那么 ( )
那么 ( )


 (
(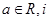 为虚数单位)是纯虚虚数,则
为虚数单位)是纯虚虚数,则 ( )
( )
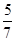
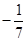

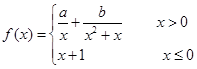 在R上连续,则
在R上连续,则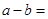 ( )
( ) 展开式中含有
展开式中含有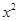 项,则
项,则 可能的取值是
可能的取值是 且目标函数
且目标函数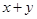 的最大值为7,最小值为1,则
的最大值为7,最小值为1,则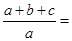
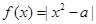 在区间[-1,1]上的最大值
在区间[-1,1]上的最大值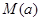 的最小值是 ( )
的最小值是 ( )
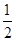
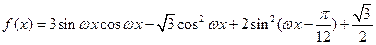 (其中
(其中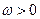 )的最小正周期为
)的最小正周期为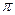 。
。 的单调递增区间;
的单调递增区间; 中,
中,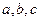 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知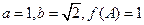 ,求角C。
,求角C。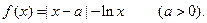
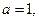 求
求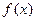 的单调区间及
的单调区间及 ,求
,求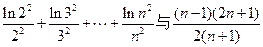 的大小,
的大小, ,并证明你的结论。
,并证明你的结论。 粤公网安备 44130202000953号
粤公网安备 44130202000953号