已知函数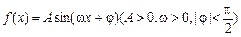 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(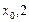 )和(
)和(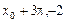 ).
).
(I)求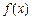 的解析式;
的解析式;
(II)用列表作图的方法画出函数y=f(x)在长度为一个周期的闭区间上的图象.
相关知识点
推荐套卷
已知函数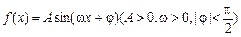 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(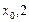 )和(
)和(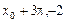 ).
).
(I)求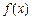 的解析式;
的解析式;
(II)用列表作图的方法画出函数y=f(x)在长度为一个周期的闭区间上的图象.