高中数学简单的等周问题试题

设直线 $m$与平面 $\alpha$相交但不垂直，则下列说法中正确的是

A．	在平面 $\alpha$内有且只有一条直线与直线 $m$垂直
B．	过直线 $m$有且只有一个平面与平面 $\alpha$垂直
C．	与直线 $m$垂直的直线不可能与平面 $\alpha$平行
D．	与直线 $m$平行的平面不可能与平面 $\alpha$垂直

下列4个命题，其中的真命题是              (    ) 
 ㏒_1/2x>㏒_1/3x
㏒_1/2x ㏒_1/3x

A．（

B．

C．

D．

下列命题中：
①若为两个命题，则“且为真”是“或为真”的必要不充分条件；
②若为：∈R，,则为：x∈R，;
③若,则. 所有正确命题的个数为        （  ）

A．0

B．1

C．2

D．3

命题“若方程的两根均大于0，则”的一个等价命题是（   ）

A．若，则方程的两根均大于0；

B．若方程的两根均不大于0，则；

C．若，则方程的两根均不大于0；

D．若，则方程的两根不全大于0.

给定两个命题,：对任意实数都有恒成立；：关于的方程有实数根；如果与中有且仅有一个为真命题，求实数的取值范围

对临界值表知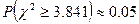.对此，四名同学做出了如下判断：
P：有95％的把握认为“这种血清能起到预防感冒的作用”：
q：若某人未使用该血清，那么他在一年中有95％的可能性得感冒；
r：这种血清预防感冒的有效率为95％；
s：这种血清预防感冒的有效率为5％；
则下列结论中正确的结论的序号是         。（把你认为正确的命题的序号都填上）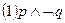
；；；；

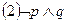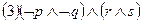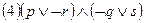已知命题：函数的图像必过定点；命题的图像关于轴对称，则函数关于直线对称，那么     （      ）

A．为真	B．为假
C．	D．

设命题：在区间上是减函数；命题：是方程的两个实根,不等式对任意实数恒成立；若为真，试求实数的取值范围。

分别指出由下列命题构成的“pq”、“pq”、“p”形式的命题的真假.
(1)p:3是9的约数,q:3是18的约数;
(2)p:菱形的对角线相等,q:菱形的对角线互相垂直;
(3)p:方程x²+x-1=0的两实根符号相同,
q:方程x²+x-1=0的两实根绝对值相等.
(4)p:是有理数,q: 是无理数.

已知命题： P：对任意,不等式恒成立；
q：函数存在极大值和极小值。
求使命题“p且q”为真命题的m的取值范围。

写出由下述各命题构成的“p或q”，“p且q”，“非p”形式的复合命题，并指出所构成的这些复合命题的真假。
（1）p：5是17的约数，q：5是15的约数.
（2）p：方程x²－1=0的解是x="1, " q：方程x²－1=0的解是x=－1,
（3）p：不等式的解集为R，q：不等式的解集为

已知； 若是的必要非充分条件，求实数的取值范围。

写出下列命题的“”命题：
（1）正方形的四边相等。
（2）平方和为的两个实数都为。
（3）若是锐角三角形， 则的任何一个内角是锐角。
（4）若，则中至少有一个为。
（5）若。

命题p：若a、b∈R，则|a|+|b|>1是|a+b|>1的充分而不必要条件；命题q：函数y=的定义域是（－∞，－1∪[3，+∞．则                                                                         （   ）

A．“p或q”为假	B．p假q真
C．p真q假	D．“p且q”为真