写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1, " q:方程x2-1=0的解是x=-1,
(3)p:不等式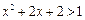 的解集为R,q:不等式
的解集为R,q:不等式 的解集为
的解集为
相关知识点
推荐套卷
写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1, " q:方程x2-1=0的解是x=-1,
(3)p:不等式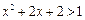 的解集为R,q:不等式
的解集为R,q:不等式 的解集为
的解集为