高中数学函数迭代试题

对于任意的两个实数对（a,b）和(c,d),规定（a,b）＝(c,d)当且仅当a＝c,b＝d;运算
“”为：，运算“”为：
，设，若
则(     ).

A．

B．

C．

D．

计算：=              

设定义在上的函数，若函数与的定义域与值域都相同，则实数的取值范围为         ．

用表示两个实数中的最小值．已知函数，若函数至少有3个零点，则的最小值为 （    ）

A．

B．

C．

D．

给出定义：若(其中为整数)，则叫做离实数最近的整数，记作，即.在此基础上给出下列关于函数的四个命题：
①的定义域是，值域是；
②点是的图像的对称中心，其中；
③函数的最小正周期为；
④函数在上是增函数．
则上述命题中真命题的序号是            ．

设函数，则函数的零点的个数为(     )

A．4

B．5

C．6

D．7

已知抛物线 ，
（1）用配方法确定它的顶点坐标、对称轴；
（2）取何值时，随增大而减小？
（3）取何值时，抛物线在轴上方？

设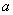是实数．若函数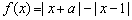是定义在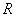上的奇函数，但不是偶函数，则函数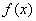的递增区间为__________;

设，则     .

已知函数．
（1）当时，求的单调区间，如果函数仅有两个零点，求实数的取值范围；
（2）当时，试比较与1的大小.

函数的值域是（  ）

A．

B．

C．

D．

定义：函数f(x)的定义域为D,如果对于任意的x1∈D，存在唯一的x2∈D，使得 (其中c为常数）成立，则称函数f(x)在D上的几何均值为c则 下列函数在其定义域上的“几何均值”可以为2的是

A．y = x^2 + 1	B．y =" sinx" + 3
C．y=ex(e为自然对数的底）	D．y= |lnx|

函数的定义域是(　　)

A．(－，－1)	B．(1，＋)
C．(－1，1)∪(1，＋)	D．(－，＋)

已知的反函数，若，则的图象大致是（　 ）

设定义在实数集上函数满足：，且当时，，则有(　　)

A．	B．
C．	D．