高中数学函数迭代试题

已知抛物线 ，
（1）用配方法确定它的顶点坐标、对称轴；
（2）取何值时，随增大而减小？
（3）取何值时，抛物线在轴上方？

设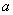是实数．若函数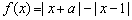是定义在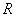上的奇函数，但不是偶函数，则函数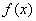的递增区间为__________;

定义域是一切实数的函数，其图像是连续不断的，且存在常数()
使得对任意实数都成立，则称是一个“—伴随函数”． 有
下列关于“—伴随函数”的结论：
①是常数函数中唯一一个“—伴随函数”；
②“—伴随函数”至少有一个零点；
③是一个“—伴随函数”；
其中正确结论的个数是 （    ）

A．1个；

B．2个；

C．3个；

D．0个；

已知函数．
（1）当时，求的单调区间，如果函数仅有两个零点，求实数的取值范围；
（2）当时，试比较与1的大小.

设函数为奇函数，则           ．

定义：函数f(x)的定义域为D,如果对于任意的x1∈D，存在唯一的x2∈D，使得 (其中c为常数）成立，则称函数f(x)在D上的几何均值为c则 下列函数在其定义域上的“几何均值”可以为2的是

A．y = x^2 + 1	B．y =" sinx" + 3
C．y=ex(e为自然对数的底）	D．y= |lnx|

函数的定义域是(　　)

A．(－，－1)	B．(1，＋)
C．(－1，1)∪(1，＋)	D．(－，＋)

已知的反函数，若，则的图象大致是（　 ）

已知函数，
（1）若是偶函数，求的值。
（2）设，，求的最小值。

设函数，记的导函数，的导函数
，
的导函数，…，的导函数，.
（1）求；
（2）用n表示；
（3）设，是否存在使最大？证明你的结论.

设二次函数f(x)=x²+bx+c,满足f(x+3)=f(3-x),则使f(x)>c-8的x的取值范围为(　　)

A．(-∞,2)	B．(4,+∞)
C．(-∞,2)∪(4,+∞)	D．(2,4)

已知函数的图象是连续不断的，有如下对应值表：

则函数在区间        有零点.

设函数对任意满足，且，则的值为     。 

设函数
（Ⅰ）当时，求函数的极值；
（Ⅱ）当时，讨论函数的单调性.
（Ⅲ）若对任意及任意，恒有 成立，求实数的取值范围.

已知函数的定义域为，部分对应值如下表，的导函数的图象如图所示. 下列关于的命题：

①函数的极大值点为，；②函数在上是减函数；③如果当时，的最大值是2，那么的最大值为4；
④当时，函数有个零点；⑤函数的零点个数可能为0、1、2、3、4个．其中正确命题的序号是                           ．