已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,不等式
时,不等式 成立,若
成立,若 ,
, ,
, ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).
| A.a>b>c | B.c>b>a | C.c>a>b | D.a>c>b |
关于函数 ,
, 有下面四个结论:
有下面四个结论:
(1) 是奇函数; (2)
是奇函数; (2) 恒成立;
恒成立;
(3) 的最大值是
的最大值是 ; (4)
; (4)  的最小值是
的最小值是 .
.
其中正确结论的是_______________________________________.
设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
已知函 数 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;
(2)若对于 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围;
(3)记 .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
, ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 内的点,则实数
内的点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数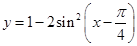 是( )
是( )
A.最小正周期为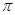 的偶函数 的偶函数 |
B.最小正周期为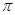 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |