已知函数 在
在 处取得极值,且
处取得极值,且 恰好是
恰好是 的一个零点.
的一个零点.
(Ⅰ)求实数 的值,并写出函数
的值,并写出函数 的单调区间;
的单调区间;
(Ⅱ)设 、
、 分别是曲线
分别是曲线 在点
在点 和
和 (其中
(其中 )处的切线,且
)处的切线,且 .
.
①若 与
与 的倾斜角互补,求
的倾斜角互补,求 与
与 的值;
的值;
②若 (其中
(其中 是自然对数的底数),求
是自然对数的底数),求 的取值范围.
的取值范围.
设函数 .
.
(1)若x= 时,
时, 取得极值,求
取得极值,求 的值;
的值;
(2)若 在其定义域内为增函数,求
在其定义域内为增函数,求 的取值范围;
的取值范围;
(3)设 ,当
,当 =-1时,证明
=-1时,证明 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明 (
( ).
).
已知函数
(1)当 时,求
时,求 在
在 上的最小值;
上的最小值;
(2)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
函数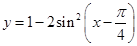 是( )
是( )
A.最小正周期为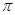 的偶函数 的偶函数 |
B.最小正周期为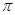 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |