高中数学函数迭代试题

函数在上是增函数，则（ ）
A ＞0      B  ＜0    C  ＞-1      D  ＜-1

若函数是R上的增函数，则实数的取值范围为（   ）

A．

B．

C．

D．

设f(x)为周期是2的奇函数，当时，f(x)=x(x+1),则当时，f(x)的表达式为

A．（x-5）(x-4)

B．(x-6)(x-5)

C．(x-6)(5-x)

D．(x-6)(7-x)

已知函数在处取得极大值，在处取得极小值，满足，，则的取值范围是

A．

B．

C．

D．

（本小题满分12分）
已知函数,
(1)  若存在实数，使得，求实数的取值范围；
(2)  设，且在区间上单调递增，求实数的取值范围。

设，则使函数的定义域为且为奇函数的所有的值为

A．

B．

C．

D．

已知，则=

A．3

B．4

C．3.5

D．4.5

已知函数,，设.
（1）求的单调区间；
（2）若以图象上任意一点为切点的切线的斜率
恒成立，求实数的最小值.
（3）是否存在实数，使得函数的图象与的图
象恰好有四个不同的交点？若存在，求出的取值范围，若不存在，说明理由.

已知a>b，二次三项式ax² +2x +b≥0对于一切实数x恒成立，又，使成立，则的最小值为（   ）

A．1

B．

C．2

D．2

函数的一个单调减区间为_______．

已知，则　　　　　　　　　　　

（本小题满分12分）
已知函数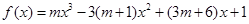其中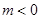
（1）、若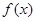的单调增区间是（0.1），求m的值
（2）、当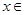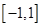时，函数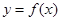的图像上任意一点的切线斜率恒大于3m，求m的取值范围.

已知函数是定义在R上的奇函数，当时，
（1）求的解析式
（2）解关于的不等式

已知是函数的两个零点，函数的最小值为，记
（ⅰ）试探求之间的等量关系（不含）；
（ⅱ）当且仅当在什么范围内，函数存在最小值？
（ⅲ）若，试确定的取值范围。

对于区间上有意义的两个函数如果有任意，均有则称与在上是接近的,否则称与在上是非接近的.现有两个函数与给定区间， 讨论与在给定区间上是否是接近的．