[辽宁]2013届辽宁省五校协作体高三上学期期中考试文科数学试卷
设全集U=R,集合P=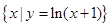 ,集合Q=
,集合Q=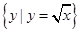 ,则集合P∩
,则集合P∩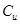 Q为( )
Q为( )
| A.{x︱-1﹤x≤0,x∈R} | B.{x︱-1﹤x﹤0,x∈R} |
| C.{x︱x﹤0,x∈R} | D.{x︱x>-1,x∈R} |
下列命题中错误的个数是( )
①命题“若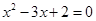 则x=1”的否命题是“若
则x=1”的否命题是“若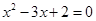 则x≠1”
则x≠1”
②命题P: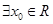 ,使
,使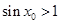 ,则
,则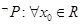 ,使
,使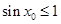
③若P且q为假命题,则P、q均为假命题
④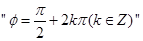 是函数
是函数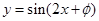 为偶函数的充要条件
为偶函数的充要条件
| A.1 | B.2 | C.3 | D.4 |
若点P(3,-1)为圆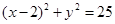 的弦AB的中点,则直线AB的方程为( )
的弦AB的中点,则直线AB的方程为( )
| A.x+y-2=0 | B.2x-y-7=0 | C.2x+y-5=0 | D.x-y-4=0 |
若曲线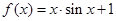 在
在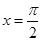 处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
| A.-2 | B.-1 | C.1 | D.2 |
已知m、n是两条不同的直线,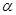 、
、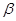 、
、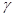 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )
A.若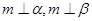 则 则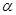 ∥ ∥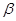 |
B.若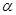 ∥ ∥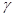 , ,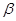 ∥ ∥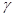 则 则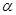 ∥ ∥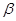 |
C.若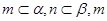 ∥n则 ∥n则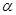 ∥ ∥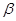 |
D.若m、n是异面直线,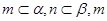 ∥ ∥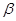 ,n∥ ,n∥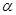 则 则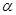 ∥ ∥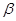 |
函数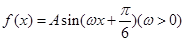 的图像与x轴的交点的横坐标构成一个公差为
的图像与x轴的交点的横坐标构成一个公差为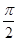 的等差数列,要得到函数
的等差数列,要得到函数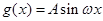 的图像,只需将
的图像,只需将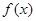 的图像( )
的图像( )
A向左平移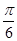 个单位 B.向右平移
个单位 B.向右平移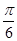 个单位
个单位
C.向左平移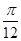 个单位 D.向右平移
个单位 D.向右平移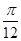 个单位
个单位
函数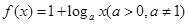 的图像恒过定点A,若点A在直线
的图像恒过定点A,若点A在直线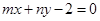 上,其中mn>0,则
上,其中mn>0,则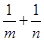 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
已知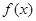 是R上最小正周期为2的周期函数,且当
是R上最小正周期为2的周期函数,且当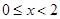 时,
时,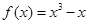 ,则函数
,则函数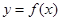 在区间
在区间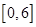 上的图像与x轴的交点个数为( )
上的图像与x轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
如图所示是一个几何体的三视图(单位:cm),主视图和左视图是底边长为4cm,腰长为 的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是__________
的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是__________
设数列 的前n项和为
的前n项和为 ,已知数列
,已知数列 是首项和公比都为3的等比数列,则数列
是首项和公比都为3的等比数列,则数列 的通项公式为
的通项公式为 =_____________________
=_____________________
(本小题满分10分)
已知圆M过两点C(1,-1)、D(-1,1)且圆心M在直线x+y-2=0上。
(1)、求圆M的方程
(2)、设P是直线3x+4y+8=0上的动点,PA、PB是圆M的两条切线,A、B为切点,求四边形PAMB的面积的最小值。
(本小题满分12分)
已知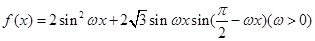 最小正周期为
最小正周期为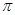
(1).求函数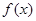 的单调递增区间及对称中心坐标
的单调递增区间及对称中心坐标
(2).求函数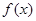 在区间
在区间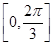 上的取值范围。
上的取值范围。
(本小题满分12分)
已知数列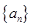 的前n项和为
的前n项和为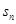 ,满足
,满足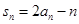
(1)求数列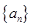 的通项公式
的通项公式
(2)设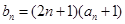 ,求数列
,求数列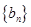 的前n项和
的前n项和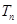 。
。
(本小题满分12分)
在四棱柱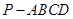 中,底面
中,底面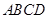 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC=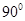 ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD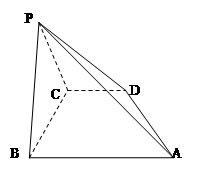
(1)求证:AB⊥平面PBC
(2)求三棱锥C-ADP的体积
(3)在棱PB上是否存在点M使CM∥平面PAD?
若存在,求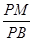 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。
(本小题满分12分)
若a、b、c是△ABC三个内角A、B、C所对边,且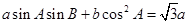
(1)求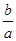
(2)当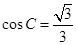 时,求
时,求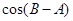 的值
的值
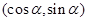 在直线
在直线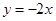 上,则
上,则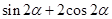 =( )
=( )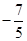
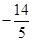
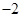
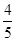
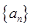 是等差数列,
是等差数列,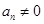 若
若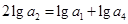 ,则
,则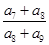 的值是( )
的值是( )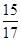
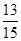
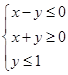 ,则
,则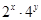 的最大值是( )
的最大值是( )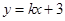 与圆
与圆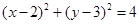 相交于M、N两点,若
相交于M、N两点,若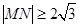 ,则k的取值范围为( )
,则k的取值范围为( )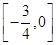
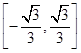
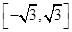
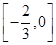
 满足
满足 ,则
,则 ___________
___________ ,则角B的值为____________
,则角B的值为____________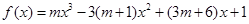 其中
其中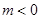
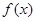 的单调增区间是(0.1),求m的值
的单调增区间是(0.1),求m的值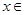
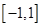 时,函数
时,函数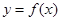 的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
的图像上任意一点的切线斜率恒大于3m,求m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号