高中数学函数迭代填空题

函数的一个零点是，则另一个零点是_________．

对a,b∈R,记max(a,b)=函数f(x)=max(|x+1|,-x²+1)的最小值是　　　.

若，则满足不等式的ｍ的取值范围为　　　．

若函数对于上的任意都有，则实数的取值范围是     ．

给出以下四个结论：
①函数的对称中心是
②若不等式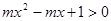对任意的x∈R都成立，则；
③已知点与点Q(l,0)在直线两侧，则；
④若将函数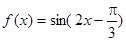的图像向右平移个单位后变为偶函数，则的最小值是．
其中正确的结论是____________（写出所有正确结论的编号）．

关于的方程恰有个不同的实根，则的取值范围是________.

给出下列五个命题中，其中所有正确命题的序号是_______.
①函数的最小值是3
②函数若且，则动点到直线的
最小距离是.
③命题“函数当”是真命题.
④函数的最小正周期是1的充要条件是.
⑤已知等差数列的前项和为，为不共线的向量，又
若，则.

对于函数，
①过该函数图像上一点（）的切线的斜率为
②函数的最小值为    
③该函数图像与轴有4个交点
④函数在上为减函数，在上也为减函数
其中正确命题的序号为                  

已知函数，则___．

对于函数f(x)，若在其定义域内存在两个实数a，b(a＜b)，使当x∈[a，b]时，f(x)的值域也是[a，b]，则称函数f(x)为“布林函数”，区间[a，b]称为函数f(x)的“等域区间”.
（1）布林函数的等域区间是        .
（2）若函数是布林函数，则实数k的取值范围是          .

已知定义在区间[0，1]上的函数图象如图所示，对于满足0＜＜＜1的
任意，给出下列结论：
①②③；
其中正确结论的序号是       ．（把所有正确结论的序号都填写在横线上）

已知函数，对任意的，都有，则最大的正整数为     .

定义在R上的函数是增函数，且函数的图像关于（3，0）成中心对称，若满足不等式，当时，则的取值范围为____.

若存在正数，使成立，则实数的取值范围是          .

定义在上的函数满足.若当时.,则当时,=        .