高中数学函数迭代填空题

已知函数是定义在上的奇函数，，且在上是增函数，则下列结论：①若且，则；
②若，则；③若方程内恰有四个不同的解，则。
其中正确的命题序号有        

已知,若,则的取值范围是

某产品的总成本C（万元）与产量x(台)之间有函数关系式：C=3000+20x-0.1x²,其中x(0,240)。若每台产品售价为25万元，则生产者不亏本的最低产量为   台。

已知，则         

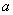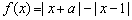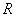设是实数．若函数是定义在上的奇函数，但不是偶函数，则函数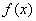的递增区间为__________;

设f(x)＝，若f(f(1))＝1，则a＝________.

函数在区间[0,4]的最大值是            

设函数的定义域为，若存在非零实数使得对于任意，有，且，则称为上的高调函数.如果定义域是的函数为上的高调函数，那么实数的取值范围是　  .     

已知函数是上的偶函数，若对于，都有，且当时， ，的值为             ． 

在弹性限度内，拉伸弹簧所用的力与弹簧伸长的长度成正比．如果的力能使弹簧伸长，则把弹簧从平衡位置拉长（在弹性限度内）时所做的功为     （单位：焦耳）.

已知函数的定义域为，部分对应值如下表，的导函数的图象如图所示. 下列关于的命题：

①函数的极大值点为，；②函数在上是减函数；③如果当时，的最大值是2，那么的最大值为4；
④当时，函数有个零点；⑤函数的零点个数可能为0、1、2、3、4个．其中正确命题的序号是                           ．

已知是上最小正周期为2的周期函数，且当时，，则函数的图象在区间上与轴的交点的个数为         ．

函数的最小值为_____________

函数对于总有≥0 成立，则=    　 ．

某商场对顾客实行购物优惠活动，规定购物付款总额要求如下：
①如果一次性购物不超过元，则不给予优惠；
②如果一次性购物超过元但不超过元，则按标价给予折优惠；
③如果一次性购物超过元，则元按第②条给予优惠，剩余部分给予折优惠．
甲单独购买商品实际付款元，乙单独购买商品实际付款元，若丙一次性购买，两件商品，则应付款           元．