高中数学函数迭代解答题

(本小题满分14分）
在矩形ABCD中，已知，在AB、AD、CD、CB上分别
截取AE、AH、CG、CF都等于，
（1）将四边形EFGH的面积S表示成的函数，并写出函数的定义域
（2）当为何值时，四边形EFGH的面积最大？并求出最大面积

（本小题满分12分）
已知函数f(x)＝(1＋x)²－ln(1＋x)，
(1)求f(x)的单调区间；(2)若x∈时，f(x)<m恒成立，求m的取值范围．

附加题（本大题共两个小题，每个小题10分，满分 20分，省级示范性高中要
把该题成绩计入总分，普通高中学生选作）
已知，
（1）判断函数在区间（-∞，0）上的单调性，并用定义证明；
（2）画出该函数在定义域上的图像.（图像体现出函数性质即可）

（本小题满分13分）已知定义域为的函数是奇函数.
（1）求的值；（2）判断函数的单调性;
（3）若对任意的，不等式恒成立，求k的取值范围．

已知函数．
（1）解关于的不等式；
（2）若对，恒成立，求的取值范围．

有一个公益广告说：“若不注意节约用水，那么若干年后，最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过5吨时，每吨水费收基本价1.3元；若超过5吨而不超过6吨时，超过部分的水费加收200%；若超过6吨而不超过7吨时，超过部分的水费加收400%。设某人本季度实际用水量为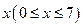吨，应交水费为f(x)，
（1）求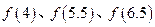的值；
（2）试求出函数f(x)的解析式。

函数在（-1，1）上是减函数，且为奇函数，满足
，试求的范围。

已知，，，比较与的大小。

已知函数有如下性质：如果常数，那么该函数在上是减函数，在上是增函数。
（1）如果函数在上是减函数，在上是增函数，求的值。
（2）设常数，求函数的最大值和最小值；

．(本小题满分14分)
设实数、同时满足条件：，且,
(1)求函数的解析式和定义域；
(2)判断函数的奇偶性；
(3)若方程恰有两个不同的实数根，求的取值范围

（本小题满分10分）设函数．
（Ⅰ）当时，求函数的定义域；
（Ⅱ）若函数的定义域为，试求实数的取值范围．

（满分12分）已知恒不为0，对于任意
等式恒成立.求证：是偶函数.

（本小题满分12分）
设p：实数x满足
（1）若为真，求实数x的取值范围；
（2）若p是q的充分不必要条件，求实数a的取值范围.

（本小题满分12分）(注意:在试题卷上作答无效)
已知函数.
(Ⅰ)若曲线在和处的切线互相平行，求的值；
(Ⅱ)求的单调区间；
(Ⅲ)设，若对任意，均存在，使得，求的取值范围.

已知函数f(x)＝log_a(x＋1)，g(x)＝2log_a(2x＋t)(t∈R)，其中x∈[0,15]，a＞0，且a≠1.
(1)若1是关于x的方程f(x)－g(x)＝0的一个解，求t的值；
(2)当0＜a＜1时，不等式f(x)≥g(x)恒成立，求t的取值范围；