(本小题满分14分）
在矩形ABCD中，已知
，在AB、AD、CD、CB上分别
截取AE、AH、CG、CF都等于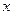
，
（1）将四边形EFGH的面积S表示成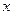的函数，并写出函数的定义域
（2）当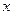为何值时，四边形EFGH的面积最大？并求出最大面积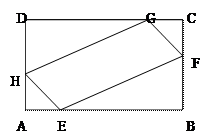
相关试题
．
的定义域为A，求集合A； 
）上单调性，并用单调性的定义加以证明．
，
．
在
上是增函数，求实数
的取值范围；
，使得关于
的方程
有三个不相等的实数根，求实数
的取值范围．
，函数
的值恒大于零，求
的取值范围．
，函数
的取值范围．
．
的奇偶性；
；
，
，且
，
，求
，
的值．
是边长为
的正三角形，记
（
）左侧的图形的面积为
．试求
的图象．
相关知识点
推荐套卷
(本小题满分14分）
在矩形ABCD中，已知，在AB、AD、CD、CB上分别
截取AE、AH、CG、CF都等于，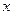
（1）将四边形EFGH的面积S表示成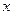的函数，并写出函数的定义域
（2）当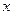为何值时，四边形EFGH的面积最大？并求出最大面积
粤公网安备 44130202000953号