函数 的定义域为D,若对于任意
的定义域为D,若对于任意 ,当
,当 时都有
时都有 ,则称函数
,则称函数 在D上为非减函数,设函数
在D上为非减函数,设函数 在[0,1]上为非减函数,且满足以下三个条件:①
在[0,1]上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③ ,则
,则 等于( )
等于( )
A. |
B. |
C.1 | D. |
我国古代数学名著《九章算术》中 “开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式 ,人们还用过一些类似的近似公式.根据π=3.14159…判断,下列近似公式中最精确的一个是
,人们还用过一些类似的近似公式.根据π=3.14159…判断,下列近似公式中最精确的一个是
A. |
B. |
C. |
D. |
设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“类对称点”,则
的“类对称点”,则 的“类对称点”的横坐标是
的“类对称点”的横坐标是
| A.1 | B. |
C.e | D. |
定义在实数集 上的函数
上的函数 的图像是连续不断的,若对任意的实数
的图像是连续不断的,若对任意的实数 ,存在常数
,存在常数 使得
使得 恒成立,则称
恒成立,则称 是一个“关于
是一个“关于 函数”,下列“关于
函数”,下列“关于 函数”的结论正确的是( )
函数”的结论正确的是( )
A. 不是 “关于 不是 “关于 函数” 函数” |
B. 是一个“关于 是一个“关于 函数” 函数” |
C.“关于 函数”至少有一个零点 函数”至少有一个零点 |
D. 不是一个“关于 不是一个“关于 函数” 函数” |
设 和
和 是定义在同一个区间
是定义在同一个区间 上的两个函数,若函数
上的两个函数,若函数 在
在 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”.若
称为“关联区间”.若 与
与 在
在 上是“关联函数”,则
上是“关联函数”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在实数集 中定义一种运算“
中定义一种运算“ ”,对任意
”,对任意 ,
, 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质:
(1)对任意 ,
, ; (2)对任意
; (2)对任意 ,
, .
.
则函数 的最小值为
的最小值为
A. |
B. |
C. |
D. |
定义区间 的长度均为
的长度均为 ,用
,用 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,记
,记 ,设
,设 ,若用
,若用 表示不等式
表示不等式 解集区间的长度,则当
解集区间的长度,则当 时有( )
时有( )
A. |
B. |
C. |
D. |
对于三次函数 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数 ,则
,则 =( )
=( )
| A.2011 | B.2012 | C.2013 | D.2014 |
对于任意的两个实数对 和
和 规定
规定 当且仅当
当且仅当 ;
;
运算“ ”为:
”为: ,运算“
,运算“ ”为:
”为: ,设
,设 ,若
,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设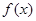 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数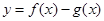 在
在 上有两个不同零点,则称
上有两个不同零点,则称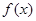 与
与 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”,若
称为“关联区间”,若 和
和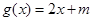 在
在 上是“关联函数”,则
上是“关联函数”,则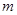 的范围为( )
的范围为( )
A. |
B.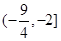 |
C. |
D.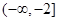 |
对于函数 和
和 ,设
,设 ,
, ,若存在
,若存在 、
、 ,使得
,使得 ,则称
,则称 互为“零点关联函数”.若函数
互为“零点关联函数”.若函数 与
与 互为“零点关联函数”,则实数
互为“零点关联函数”,则实数 的取值范围为( ).
的取值范围为( ).
A. |
B. |
C. |
D. |
一只蚂蚁从正方体 的顶点
的顶点 处出发,经正方体的表面,按最短路线爬行到达顶点
处出发,经正方体的表面,按最短路线爬行到达顶点 位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )
位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )
| A.①② | B.①③ | C.③④ | D.②④ |
定义域为R的函数 ,若对任意两个不相等的实数
,若对任意两个不相等的实数 ,都有
,都有 ,则称函数为“H函数”,现给出如下函数:
,则称函数为“H函数”,现给出如下函数:
① ②
② ③
③ ④
④
其中为“H函数”的有( )
| A.①② | B.③④ | C.②③ | D.①②③ |