高中数学一阶、二阶线性常系数递归数列的通项公式试题

数列中,,若存在实数,使得数列为
等差数列,则=_________.

如图，将圆分成n个区域，用3种不同颜色给每一个区域染色，要求相邻区域颜色互异，把不同的染色方法种数记为。求

（1）及与的关系式；
（2）数列的通项公式，并证明：

对于项数为的有穷数列数集，记，即为、、、中的最大值，并称数列是的控制数列.如、、、、的控制数列是、、、、.
（1）若各项均为正整数的数列的控制数列为、、、、，写出所有的；
（2）设是的控制数列，满足（为常数，、、、）.求证：.

在一个数列中，如果对任意,都有为常数，那么这个数列叫做等积数列，叫做这个数列的公积．已知数列是等积数列，且，公积为，记的前项和为，则：
（1）          ．
（2）           ．

设不等式组所表示的平面区域为D_n，记D_n内的整点个数为a_n(n∈N^*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{a_n}的通项公式；
(2)记数列{a_n}的前n项和为S_n，且T_n＝.若对于一切的正整数n，总有T_n≤m，求实数m的取值范围．

有一个数阵排列如下：

则第20行从左至右第10个数字为           .

设数列{a_n}的前n项和为S_n.已知a₁＝1，＝a_n＋1－n²－n－，n∈N^*.
(1)求a₂的值；
(2)求数列{a_n}的通项公式；
(3)证明：对一切正整数n，有.

对于各项均为整数的数列，如果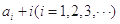为完全平方数，则称数列具有“P性质”，如果数列不具有“P性质”，只要存在与不是同一数列的，且同时满足下面两个条件：①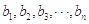是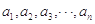的一个排列；②数列具有“P性质”，则称数列具有“变换P性质”，下面三个数列：
①数列1，2，3，4，5； ②数列1，2，3， ，11,12； ③数列的前n项和为.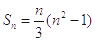
其中具有“P性质”或“变换P性质”的有(     )

A．③

B．①③

C．①②

D．①②③

已知a_n＝
(1)求数列{a_n}的前10项和S₁₀；
(2)求数列{a_n}的前2k项和S_2k.

在轴的正方向上，从左向右依次取点列 ，以及在第一象限内的抛物线上从左向右依次取点列，使（）都是等边三角形，其中是坐标原点，则第2005个等边三角形的边长是      ．

如果有穷数列满足条件: 即，我们称其为“对称数列”．例如:数列1，2，3，3，2，1 和数列1，2，3，4，3，2，1都为 “对称数列”。已知数列是项数不超过的“对称数列”，并使得依次为该数列中连续的前项，则数列的前2009项和所有可能的取值的序号为
① 
②
③ 
④

A．①②③

B．②③④

C．①②④

D．①③④

对于一个有限数列，定义的蔡查罗和（蔡查罗是一位数学家）为，其中．若一个99项的数列（的蔡查罗和为1000，那么100项数列的蔡查罗和为（  ）

A．993

B．995

C．997

D．999

对于给定数列，如果存在实常数使得对于任意都成立，我们称数列是 “线性数列”．
（1）若，，，数列、是否为“线性数列”？若是，指出它对应的实常数，若不是，请说明理由；
（2）证明：若数列是“线性数列”，则数列也是“线性数列”；
（3）若数列满足，，为常数．求数列前项的和．

已知数列满足，给出下列命题：
①当时，数列为递减数列
②当时，数列不一定有最大项
③当时，数列为递减数列
④当为正整数时，数列必有两项相等的最大项
请写出正确的命题的序号____

已知正项数列满足：，数列的前项和为，且满足，.
（1）求数列和的通项公式；
（2）设，数列的前项和为，求证：.