(本小题16分)如图所示,数列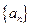 的前
的前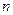 项的和
项的和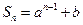 ,
,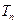 为数列
为数列 的前
的前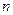 项的和,且
项的和,且 .
.
(1)求数列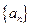 、
、 的通项公式;
的通项公式;
(2)找出所有满足: 的自然数
的自然数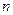 的值(不必证明);
的值(不必证明);
(3)若不等式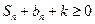 对于任意的
对于任意的 ,
,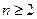 恒成立,求实数
恒成立,求实数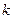 的最小值,并求出此时相应的
的最小值,并求出此时相应的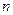 的值.
的值.
数列{an}满足an+an+1= (n∈N*),且a1=1,Sn是数列{an}的前n项和,则S21=( )
(n∈N*),且a1=1,Sn是数列{an}的前n项和,则S21=( )
A. |
B.6 |
| C.10 | D.11 |
已知等差数列 的公差为
的公差为 ,且
,且 ,若
,若 ,则
,则 为
为
| A.12 | B.10 | C.8 | D.4 |
已知数列 的前
的前 项和
项和 和通项
和通项 满足
满足 数列
数列 中,
中,
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)数列 满足
满足 是否存在正整数
是否存在正整数 ,使得
,使得 时
时 恒成立?若存在,求
恒成立?若存在,求 的最小值;若不存在,试说明理由.
的最小值;若不存在,试说明理由.
已知数列{an}的前n项和为Sn,点(n,)在直线y=x+上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
定义:在数列{an}中,若满足-=d(n∈N*,d为常数),我们称{an}为“比等差数列”.已知在“比等差数列”{an}中,a1=a2=1,a3=2,则的个位数字是( )
| A.3 | B.4 | C.6 | D.8 |