高中数学不定方程和方程组试题

设分别是方程和的根（其中）, 则的取值范围是（    ）

A．

B．

C．

D．

（本小题满分12分）定义的零点为的不动点，已知函数
．
（Ⅰ）当时，求函数的不动点；
（Ⅱ）对于任意实数，函数恒有两个相异的不动点，求实数的取值范围；
（Ⅲ）若函数只有一个零点且，求实数的最小值．

已知函数，的单调增区间为           ；若有三个不相等的实根，则m=            ，且三个实根的和是              。

（本题满分14分，第1小题6分，第2小题8分）
已知函数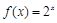的反函数为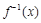
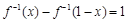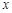（1）若，求实数的值；
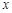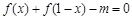（2）若关于的方程在区间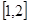内有解，求实数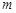的取值范围；

函数的零点所在的大致区间是（  ）

A．

B．

C．

D．

已知，分析该函数图象的特征，若方程一根大于3，另一根小于2，则下列推理不一定成立的是 （   ）

A．

B．

C．

D．

若关于的方程有四个不同的实数解，则的取值范围是      .

函数（  ）

A．

B．

C．

D．

设f（x）为定义在R上的奇函数，当x≥0时，f（x）=2^x+2x+b（b为常数），则f（﹣1）=（　　）

A．﹣3

B．﹣1

C．1

D．3

对于函数，有下列4个结论：
①任取，都有恒成立；
②，对于一切恒成立；
③函数有3个零点；
④对任意，不等式恒成立．
则其中所有正确结论的序号是            .

（本小题满分13分）设，函数，函数，.
（Ⅰ）当时，写出函数零点个数，并说明理由；
（Ⅱ）若曲线与曲线分别位于直线的两侧，求的所有可能取值.

，用记号 表示不小于实数的最小整数，例如，，；则函数的所有零点之和为       .

设三次函数的导函数,且,则函数的零点个数为（   ）

A．0

B．1

C．2

D．3

．下列说法：
①函数的零点只有1个且属于区间；
②若关于的不等式恒成立，则；
③函数的图像与函数的图像有3个不同的交点；
④函数的最小值是1．
正确的有          ．（请将你认为正确说法的序号都写上）

已知命题；命题若，则有实数解.那么下列命题中是真命题的是（  ）

A．

B．

C．

D．且