高中数学不定方程和方程组解答题

已知为常数，，函数，且方程有等根．
（1）求的解析式及值域；
（2）设集合，，若，求实数的取值范围；
（3）是否存在实数，使的定义域和值域分别为和？若存在，求出的值；若不存在，说明理由．

已知函数是偶函数．
（1）求k的值；
（2）若函数y=f（x）的图象与直线没有交点，求b的取值范围．
（3）设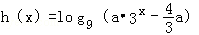，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

已知是定义在上的偶函数，当时，．
（1）求，的值；
（2）求的解析式；并画出简图；

（3）利用图象讨论方程的根的情况（只需写出结果，不要解答过程）．

已知函数．
（1）当时，求函数的零点；
（2）若函数有零点，求实数的取值范围．

（本小题满分12分）关于x的二次方程在区间上有解，求实数m的取值范围．

已知关于的方程有实根.
（1）求的值;
（2）若关于的方程的所有根均为整数，求整数的值.

已知函数 （为自然对数的底数，）．
（1）判断曲线在点处的切线与曲线的公共点个数；
（2）当时，若函数有两个零点，求a的取值范围．

关于的方程的两根分别在区间与内，求的取值范围．

设函数
（1）若函数有且只有两个零点求实数的取值范围；
（2）当时若曲线上存在横坐标成等差数列的三个点
①证明：为钝角三角形；
②试判断能否为等腰三角形并说明理由

(1)m为何值时，f(x)＝x²＋2mx＋3m＋4.
①有且仅有一个零点；②有两个零点且均比－1大；
(2)若函数f(x)＝|4x－x²|＋a有4个零点，求实数a的取值范围．

已知为整数，给出如下三个关于方程：
① ② ③
若方程①有两个相等的实数根，方程②③有且仅有一个方程有两个不相等的实数根，求的值．

已知定义在上的函数满足，当时，，且．
（Ⅰ）求的值；
（Ⅱ）当时，关于的方程有解，求的取值范围．

已知函数，．
（1）若函数在点处的切线方程为，求的值；
（2）若函数有三个不同的极值点，求的值；
（3）若存在实数，使对任意的，不等式恒成立，求正整数的最大值．

已知函数是定义在上的奇函数．当时，，且图象过点与点.
（Ⅰ）求实数的值，并求函数的解析式；
（Ⅱ）若关于的方程有两个不同的实数解，请写出实数的取值范围；
（Ⅲ）解关于的不等式，写出解集.

已知函数的图象上一点P(1，0)，且在P点处的切线与直线平行．
(1)求函数的解析式；
(2)求函数在区间[0，t](0<t<3)上的最大值和最小值；
(3)在(1)的结论下，关于x的方程在区间[1,3]上恰有两个相异的实根，求实数c的取值范围