高中数学不定方程和方程组试题

（本小题满分12分）
已知定义域为R的奇函数满足，且当时，．
（1）求在区间[－1，1]上的解析式．
（2）当m取何值时，方程在区间（0，1）上有解？

已知函数，若函数恰有两个不同的零点，则实数的取值范围为      ．

已知函数若有则的取值范围为

A．

B．

C．

D．

已知函数是偶函数．
（1）求k的值；
（2）若函数y=f（x）的图象与直线没有交点，求b的取值范围．
（3）设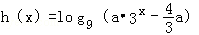，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

已知函数，若关于的函数有个不同的零点，则实数的取值范围是         ．

函数的零点所在的大致区间是（  ）

A．

B．

C．

D．

（本小题满分12分）已知定义域为的函数满足
（1）若，求；又若，求；
（2）设有且仅有一个实数，使得，求函数的解析式．

已知函数f（x）＝xln x，g（x）＝－x²＋ax－2（e为自然对数的底数，a∈R）．
（1）判断曲线y＝f（x）在点（1，f（1））处的切线与曲线y＝g（x）的公共点个数；
（2）当时，若函数y＝f（x）－g（x）有两个零点，求的取值范围．

函数f（x）=3ax﹣2a+1在[﹣1，1]上存在一个零点，则实数a的取值范围是（ ）

A．

B．a≤﹣1

C．

D．

若函数f（x）=x²+ax+1在（0，2）上有两个零点，则实数a的取值范围为     ．

设函数，则满足的的值是（ ）

A．2

B．16

C．2或16

D．－2或16

设函数的导函数为，且.
（1）求的解析式；
（2）若方程在区间上恰有两个不同的实根，求实数的取值范围.

已知是定义在上的偶函数，当时，．
（1）求，的值；
（2）求的解析式；并画出简图；

（3）利用图象讨论方程的根的情况（只需写出结果，不要解答过程）．

已知函数 （为自然对数的底数，）．
（1）判断曲线在点处的切线与曲线的公共点个数；
（2）当时，若函数有两个零点，求a的取值范围．

函数的零点一定位于区间（   ）．

A．

B．

C．

D．