某中学将
名高一新生分成水平相同的甲、乙两个“平行班”，每班
人，吴老师采用
、
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果，期末考试后，分别从两个班级中各随机抽取
名学生的成绩进行统计，作出的茎叶图如下：
记成绩不低于
分者为“成绩优秀”.
（1）在乙班样本的个个体中，从不低于
分的成绩中随机抽取
个，记随机变量
为抽到“成绩优秀”的个数，求的分布列及数学期望
；
（2）由以上统计数据填写下面
列联表，并判断有多大把握认为“成绩优秀”与教学方式有关？
| |
甲班（方式） |
乙班（方式） |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
（ 本小题满分12分） 某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动，要求每位同学至少参加一次活动．该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示
（1）从该班中任意选两名学生，求他们参加活动次数不相等的概率．
（2）从该班中任意选两名学生，用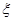
表示这两人参加活动次数之差的绝对值，求随机变量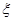的分布列及数学期望
．
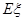（3）从该班中任意选两名学生，用
表示这两人参加活动次数之和，记“函数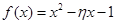
在区间（3，5）上有且只有一个零点”为事件A，求事件A发生的概率．
某煤矿发生透水事故时，作业区有若干人员被困．救援队从入口进入之后有
两条巷道通往作业区（如下图），
巷道有
三个易堵塞点，各点被堵塞的概率都是
；
巷道有
两个易堵塞点，被堵塞的概率分别为
．
（1）求巷道中，三个易堵塞点最多有一个被堵塞的概率；
（2）若巷道中堵塞点个数为
，求的分布列及数学期望
，并按照＂平均堵塞点少的巷道是较好的抢险路线＂的标准，请你帮助救援队选择一条抢险路线，并说明理由．
已知正方形
的边长为
，
、
、
、
分别是边
、
、
、
的中点．
（1）在正方形内部随机取一点
，求满足
的概率；
（2）从
、
、
、
、、、、这八个点中，随机选取两个点，记这两个点之间的距离的平方为
，求随机变量的分布列与数学期望
．
（本小题满分12分）某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
（1）从统计数据看，甲、乙两个班哪个班成绩更稳定（用数字特征说明）；
（2）若把上表数据作为学生投篮命中率，规定两个班级的1号和2号同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作
和
，试求和的分布列和数学期望．
（本小题满分12分）甲、乙两人对弈棋局，甲胜、乙胜、和棋的概率都是
，规定有一方累计2胜或者累计2和时，棋局结束。棋局结束时，若是累计两和的情形，则宣布甲乙都获得冠军；若一方累计2胜，则宣布该方获得冠军，另一方获得亚军。设结束时对弈的总局数为X．
（1）设事件A：“X=3且甲获得冠军”，求A的概率；
（2）求X的分布列和数学期望。
（本小题满分12分）已知一个袋子里装有只有颜色不同的6个小球，其中白球2个，黑球4个，现从中随机取球，每次只取一球.
（1）若每次取球后都放回袋中，求事件“连续取球四次，至少取得两次白球”的概率；
（2）若每次取球后都不放回袋中，且规定取完所有白球或取球次数达到五次就终止游戏，记游戏结束时一共取球X次，求随机变量X的分布列与期望.
某个海边旅游景点，有小型游艇出租供游客出海游玩，收费标准如下：租用时间不超过2小时收费100，超过2小时的部分按每小时100收取（不足一小时按一小时计算）．现甲、乙两人独立来该景点租用小型游艇，各租一次．设甲、乙租用不超过两小时的概率分别为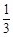
，
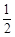；租用2小时以上且不超过3小时的概率分别为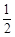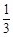，，且两人租用的时间都不超过4小时．
（Ⅰ）求甲、乙两人所付费用相同的概率；
（Ⅱ）设甲、乙两人所付的费用之和为随机变量
，求的分布列与数学期望．
（本小题满分12分）有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一组
组成.
| 第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
| 第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
| 第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量
表示密码中所含不同数字的个数.
（Ⅰ）求
；
（Ⅱ）求随机变量的分布列和它的数学期望．
(本小题满分12分)
为了普及环保知识，增强环保意识，某校从理科甲班抽取60人，从文科乙班抽取50人参加环保知识测试.
（Ⅰ）根据题目条件完成下面2×2列联表，并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.
| |
优秀人数 |
非优秀人数 |
总计 |
| 甲班 |
|
|
|
| 乙班 |
|
30 |
|
| 总计 |
60 |
|
|
（Ⅱ）现已知
三人获得优秀的概率分别为
，设随机变量
表示三人中获得优秀的人数，求的分布列及期望
.附:
，
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12．
（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．
某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5．0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有
关系，对年级名次在
名和
名的学生进行了调查，得到右表中数据，根据表中的数据，
能否在犯错的概率不超过0．05的前提下认为视力与学习成绩有关系?
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好
的护眼习惯，并且在这9人中任取3人，记名次在的学生人数为
，求的分布列和数学期望．
附：
某校高一年级有四个班，其中一、二班为数学课改班，三、四班为数学非课改班．在期末考试中，课改班与非课改班的数学成绩优秀与非优秀人数统计如表．
| |
优秀 |
非优秀 |
总计 |
| 课改班 |
|
50 |
|
| 非课改班 |
20 |
|
110 |
| 合计 |
|
|
210 |
（1）请完成上面的2×2列联表，并判断若按99%的可靠性要求，能否认为“成绩与课改有关”；
（2）把全部210人进行编号，从编号中有放回抽取4次，每次抽取1个，记被抽取的4人中的优秀人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列及数学期望Eξ．
（本小题满分13分）某学习兴趣小组开展“学生语文成绩与英语成绩的关系”的课题研究，对该校高二年级800名学生上学期期末语文和英语成绩进行统计，按优秀和不优秀进行分类．记集合A={语文成绩优秀的学生}，B={英语成绩优秀的学生}．如果用
表示有限集合M中元素的个数．已知
,
,
,其中U表示800名学生组成的全集．
（1）是否有99．9%的把握认为“该校学生的语文成绩与英语成绩优秀与否有关系” ；
（2）将上述调查所得的频率视为概率，从该校高二年级的学生成绩中，有放回地随机抽取3次，记所抽取的成绩中，语文英语两科成绩中至少有一科优秀的人数为
，求的分布列和数学期望．
附：
参考数据：
 |
0．025 |
0．010 |
0．005 |
0．001 |
 |
5．024 |
6．635 |
7．879 |
10．828 |
2014年中国汽车销售量达到2000多万辆，成为世界汽车销售的冠军，各大品牌与国内自主品牌纷纷加大促销力度，争取2015年实现新的突破．某知名品牌的汽车
店，对最近
位采用分期付款的购车者进行统计，统计结果如右表所示：已知分
期付款的频率为
．店经销一辆该品牌的汽车，顾客分
期付款， 其利润为万元；分
期或期付款其利润为
万元；分
期或
期付款，其利润为万元．用
表示经销一辆汽车的利润．
| 付款方式 |
分期 |
分期 |
分期 |
分期 |
分期 |
| 频 数 |
40 |
20 |
 |
10 |
 |
（Ⅰ）求上表中的
值；
（Ⅱ）若以频率作为概率，求事件
：“购买该品牌汽车的位顾客中，至多有位采用期付款”的概率
；
（Ⅲ）求的分布列及数学期望
．
粤公网安备 44130202000953号
