某个海边旅游景点,有小型游艇出租供游客出海游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
相关知识点
推荐套卷
 ,在
,在 中,
中, °,
°, ,
,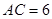 ,
, ,
, 分别是
分别是 ,
,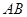 上的点,且
上的点,且 ,
, ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图
,如图 .
.
 平面
平面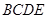 ;
;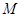 是
是 的中点,求
的中点,求 与平面
与平面 所成角的大小;
所成角的大小;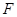 是线段
是线段 的靠近点
的靠近点 是线段
是线段 上的点,直线
上的点,直线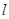 过点
过点 且垂直于平面
且垂直于平面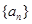 中,
中,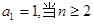 时,其前
时,其前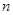 项和
项和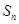 满足:
满足: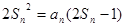 .
.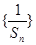 是等差数列,并用
是等差数列,并用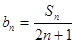 ,数列
,数列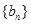 的前
的前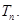 求使得
求使得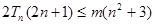 对所有
对所有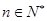 都成立的实数
都成立的实数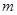 的取值范围.
的取值范围.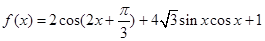 .
.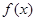 的定义域为
的定义域为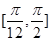 ,求
,求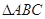 中,
中,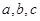 分别是
分别是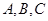 所对边, 当
所对边, 当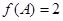 ,
,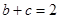 时,求
时,求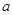 的最小值.
的最小值.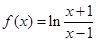
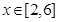
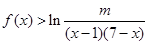 恒成立,求实数
恒成立,求实数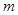 的取值范围;
的取值范围;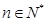 时,试比较
时,试比较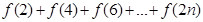 与
与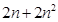 的大小关系.
的大小关系.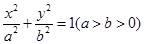 的离心率为
的离心率为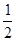 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线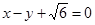 相切
相切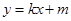 与椭圆C相交于A、B两点,且
与椭圆C相交于A、B两点,且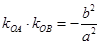 ,求证:
,求证: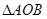 的面积为定值
的面积为定值 粤公网安备 44130202000953号
粤公网安备 44130202000953号