高中数学随机思想的发展试题

（本题满分12分 ）设不等式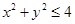确定的平面区域为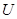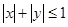，确定的平面区域为。
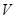（1）定义：横、纵坐标均为整数的点为“整点”，在区域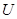内任取3个整点，求这些整点中恰有2个整点在区域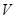的概率；
（2）在区域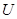内任取3个点，记这3个点在区域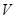的个数为，求的分布列和数学期望。

上海世博会上有一种舞台灯，外形是正六棱柱，在其每个侧面（编号分别是①②③④⑤⑥）上安装5只颜色各异的灯，每只灯正常发光的概率是0.5，若一侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用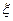表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个侧面面上恰有2个侧面需要更换的概率。
（3）写出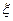的分布列，并求出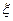的数学期望。

为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
（Ⅰ）设 $A$为事件"选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会"求事件 $A$发生的概率；
（Ⅱ）设 $X$为选出的4人中种子选手的人数，求随机变量 $X$的分布列和数学期望.

（本小题满分14分）
在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，设O为坐标原点，点P的坐标为记.
（1）求随机变量 的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望.

某电视台拟举行由选手报名参加的比赛类型的娱乐节目，选手进入正赛前需通过海选，参加海选的选手可以参加A、B、C三个测试项目，只需通过一项测试即可停止测试，通过海选．若通过海选的人数超过预定正赛参赛人数，则优先考虑参加海选测试次数少的选手进入正赛．甲选手通过项目A、B、C测试的概率为分别为、、， 且通过各次测试的事件相互独立．
（1）若甲选手先测试A项目，再测试B项目，后测试C项目，求他通过海选的概率；若改变测试顺序，对他通过海选的概率是否有影响？说明理由；
（2）若甲选手按某种顺序参加海选测试，第一项能通过的概率为p₁，第二项能通过的概率为p₂，第三项能通过的概率为p₃，设他通过海选时参加测试的次数为，求的分布列和期望（用p₁、p₂、p₃表示）；并说明甲选手按怎样的测试顺序更有利于他进入正赛．

一组数据为，，10，11，9，这组数据平均数为10，则方差的最小值为        .

（本小题15分）已知从“神七”飞船带回的某种植物种子每粒成功发芽的概率都为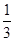，某植物研究所进行该种子的发芽实验，每次实验种一粒种子， 每次实验结果相互独立．假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．若该研究所共进行四次实验， 设表示四次实验结束时实验成功的次数与失败的次数之差的绝对值．
（1）求随机变量的分布列及的数学期望；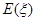
（2）记“不等式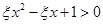的解集是实数集R”为事件A，求事件A发生的概率．

一只不透明的布袋中装有编号为1、2、3、4、5的五个大小形状完全一样的小球，现从袋中同时摸出只小球，用随机变量表示摸出的只球中的最大号码数，则随机变量的数学期望             ．

2008年5月12日，四川汶川发生8.0级特大地震，通往灾区的道路全部中断. 5月12日晚，抗震救灾指挥部决定从水路（一支队伍）、陆路（东南和西北两个方向各一支队伍）和空中（一支队伍）同时向灾区挺进．在5月13日，仍时有较强余震发生，天气状况也不利于空中航行. 已知当天从水路抵达灾区的概率是，从陆路每个方向抵达灾区的概率都是，从空中抵达灾区的概率是．
（1）求在5月13日恰有1支队伍抵达灾区的概率；
（2）求在5月13日抵达灾区的队伍数的数学期望.

为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12．

（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．

现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表．

月收入（单位百元）
频数
赞成人数

（I）由以上统计数据填下面列联表并问是否有%的把握认为“月收入以为分界点”对“楼市限购令”的态度有差异；

	月收入低于百元的人数	月收入低于百元的人数	合计
赞成
不赞成
合计

（II）若对月收入在，的被调查人中各随机选取两人进行追踪调查，记选中的人中不赞成“楼市限购令”人数为，求随机变量的分布列及数学期望．
参考数据：

（本小题满分12分）已知2件次品和3件正品混放在一起，现需要通过检测将其区分，
每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测
结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）己知每检测一件产品需要费用1 00元，设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用（单位：元），求X的分布列和均值（数学期望）．

（满分12分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为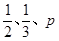。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为。
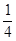（Ⅰ）求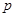的值；
（Ⅱ）设甲、乙、丙三人中破译出密码的人数为X，求X得分布列和数学期望EX。

（本小题满分12分）某城市有东西南北四个进入城区主干道的入口，在早高峰时间段，时常发生交通拥堵现象，交警部门统计11月份30天内的拥堵天数，东西南北四个主干道入口的拥堵天数分别是18天，15天，9天，15天．假设每个入口发生拥堵现象互相独立，视频率为概率．
（1）求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率；
（2）设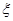表示一天中早高峰时间段发生拥堵的主干道入口个数，求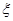的分布列和数学期望．

某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于小于为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：

测试指标
甲	3	7	20	40	20	10
乙	5	15	35	35	7	3

 
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
（1）计算新工人乙生产三件产品A，给工厂带来盈利大于或等于100元的概率；
（2）记甲乙分别生产一件产品A给工厂带来的盈利和记为X，求随机变量X的概率分布和数学期望．