(本小题15分)已知从“神七”飞船带回的某种植物种子每粒成功发芽的概率都为 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子, 每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子, 每次实验结果相互独立.假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设 表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
(1)求随机变量 的分布列及
的分布列及 的数学期望
的数学期望 ;
;
(2)记“不等式 的解集是实数集R”为事件A,求事件A发生的概率
的解集是实数集R”为事件A,求事件A发生的概率 .
.
相关知识点
推荐套卷
 和圆
和圆 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆 .
.
 ;
; ,求椭圆离心率
,求椭圆离心率 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,
, ,求证:
,求证: 为定值.
为定值.
 (
( ).
). 时,求
时,求 的极值;
的极值; 时,求
时,求 本小题共13分)
本小题共13分) 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的. 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加 课程的人数,求
课程的人数,求 的棱长为
的棱长为 ,
, 是
是 与
与 的交点,
的交点, 是
是 上一点,且
上一点,且 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
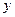
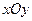 中,以
中,以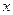 轴为始边作两个锐角
轴为始边作两个锐角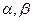 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于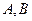 两点.已知
两点.已知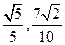 .
.
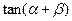 的值;
的值;
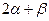 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号