设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以 表示取出次品的个数,则
表示取出次品的个数,则 的期望值
的期望值 = .
= .
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: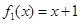 ,
,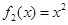 ,
, ,
,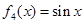 ,
,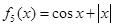 ,
,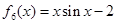 .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
某人上楼梯,每步上一阶的概率为 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第 阶的概率为
阶的概率为 .
.
(1)求 ;;
;;
(2)该人共走了5步,求该人这5步共上的阶数ξ的数学期望.
已知某一随机变量X的分布列如下:
| X |
3 |
b |
8 |
| P |
0.2 |
0.5 |
a |
且 ,则a=__________;b=__________。
,则a=__________;b=__________。
一厂家向用户提供的一箱产品共10件,其中有1件次品. 用户先对产品进行随机抽检以决定是否接受. 抽检规则如下:至多抽检3次,每次抽检一件产品(抽检后不放回),只要检验到次品就停止继续抽检,并拒收这箱产品;若3次都没有检验到次品,则接受这箱产品,按上述规则,该用户抽检次数的数学期望是___________.
设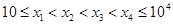 ,
, . 随机变量
. 随机变量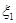 取值
取值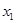 、
、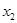 、
、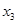 、
、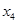 、
、 的概率均为0.2,随机变量
的概率均为0.2,随机变量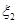 取值
取值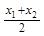 、
、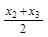 、
、 、
、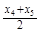 、
、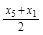 的概率也为0.2.若记
的概率也为0.2.若记 、
、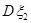 分别为
分别为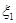 、
、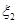 的方差,则 ( )
的方差,则 ( )
A. > >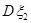 |
B. = =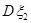 |
C. < <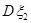 |
D. 与 与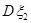 的大小关系与 的大小关系与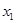 、 、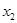 、 、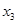 、 、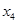 的取值有关 的取值有关 |
设某地区 型血的人数占总人口数的比为
型血的人数占总人口数的比为 ,现从中随机抽取3人.
,现从中随机抽取3人.
(1)求3人中恰有2人为 型血的概率;
型血的概率;
(2)记 型血的人数为
型血的人数为 ,求
,求 的概率分布与数学期望.
的概率分布与数学期望.
我市在夜明珠与黄柏河交汇形成的平湖水面上修建”三峡游轮中心”.其中有小型游艇出租给游客游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(本小题满分12分)某地宫有三个通道,进入地宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道,若是1号通道,则需要1小时走出地宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门。再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完地宫为止。令 表示走出地宫所需的时间。
表示走出地宫所需的时间。
(1)求 的分布列;
的分布列;
(2)求 的数学期望。
的数学期望。
某超市有奖促销,抽奖规则是:每消费满50元,即可抽奖一次.抽奖方法是:在不透明的盒内装有标着1,2,3,4,5号码的5个小球,从中任取1球,若号码大于3就奖励10元,否则无奖,之后将球放回盒中,即完成一次抽奖,则某人抽奖2次恰中20元的概率为___________;若某人消费200元,则他中奖金额的期望是_________元.
某市有一个玉米种植基地.该基地的技术员通过种植实验发现,一种品质优良的玉米种子每粒发芽的概率都为0.95,现在该种植基地播种了10000粒这种玉米种子,对于没有发芽的种子,每粒需再播种1粒,补种的种子数记为 ,则
,则 的数学期望
的数学期望 .
.
(本小题满分12分)深圳市于2014年12月29日起实施小汽车限购政策.根据规定,每年发放10万个小汽车名额,其中电动小汽车占20%,通过摇号方式发放,其余名额通过摇号和竞价两种方式各发放一半.政策推出后,某网站针对不同年龄段的申请意向进行了调查,结果如下表所示:
| 申请意向 年龄 |
摇号 |
竞价(人数) |
合计 |
|
| 电动小汽车(人数) |
非电动小汽车(人数) |
|||
| 30岁以下 (含30岁) |
50 |
100 |
50 |
200 |
| 30至50岁 (含50岁) |
50 |
150 |
300 |
500 |
| 50岁以上 |
100 |
150 |
50 |
300 |
| 合计 |
200 |
400 |
400 |
1000 |
(1)采取分层抽样的方式从30至50岁的人中抽取10人,求其中各种意向人数;
(2)在(1)中选出的10个人中随机抽取4人,求其中恰有2人有竞价申请意向的概率;
(3)用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知离散型随机变量X的分布列如表,若E(X)=0,D(X)=1,则a=________,b=________.
| X |
-1 |
0 |
1 |
2 |
| P |
a |
b |
c |
 |