[上海]2013届上海市黄浦区高三下学期二模数学试卷
一厂家向用户提供的一箱产品共10件,其中有1件次品. 用户先对产品进行随机抽检以决定是否接受. 抽检规则如下:至多抽检3次,每次抽检一件产品(抽检后不放回),只要检验到次品就停止继续抽检,并拒收这箱产品;若3次都没有检验到次品,则接受这箱产品,按上述规则,该用户抽检次数的数学期望是___________.
来源:2013届上海市黄浦区高三下学期二模数学试题
下列命题:①“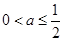 ”是“存在
”是“存在 ,使得
,使得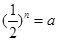 成立”的充分条件;②“
成立”的充分条件;②“ ”是“存在
”是“存在 ,使得
,使得 成立”的必要条件;③“
成立”的必要条件;③“ ”是“不等式
”是“不等式 对一切
对一切 恒成立”的充要条件. 其中所以真命题的序号是
恒成立”的充要条件. 其中所以真命题的序号是
| A.③ | B.②③ | C.①② | D.①③ |
来源:2013届上海市黄浦区高三下学期二模数学试题
已知正四棱柱 的底面边长为2,
的底面边长为2, .
.
(1)求该四棱柱的侧面积与体积;
(2)若 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的大小.
所成角的大小.
来源:2013届上海市黄浦区高三下学期二模数学试题
已知复数 (
( 为虚数单位)
为虚数单位)
(1)若 ,且
,且 ,求
,求 与
与 的值;
的值;
(2)设复数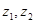 在复平面上对应的向量分别为
在复平面上对应的向量分别为 ,若
,若 ,且
,且 ,求
,求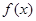 的最小正周期和单调递减区间.
的最小正周期和单调递减区间.
来源:2013届上海市黄浦区高三下学期二模数学试题
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (小时)之间满足
(小时)之间满足 ,
,
其对应曲线(如图所示)过点 .
.
(1)试求药量峰值( 的最大值)与达峰时间(
的最大值)与达峰时间( 取最大值时对应的
取最大值时对应的 值);
值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
来源:2013届上海市黄浦区高三下学期二模数学试题
设抛物线 的焦点为
的焦点为 ,经过点
,经过点 的动直线
的动直线 交抛物线
交抛物线 于点
于点 ,
,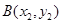 且
且 .
.
(1)求抛物线 的方程;
的方程;
(2)若 (
( 为坐标原点),且点
为坐标原点),且点 在抛物线
在抛物线 上,求直线
上,求直线 倾斜角;
倾斜角;
(3)若点 是抛物线
是抛物线 的准线上的一点,直线
的准线上的一点,直线 的斜率分别为
的斜率分别为 .求证:
.求证:
当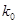 为定值时,
为定值时,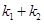 也为定值.
也为定值.
来源:2013届上海市黄浦区高三下学期二模数学试题
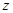 满足
满足 ,则
,则 的定义域为___________.
的定义域为___________. 过点
过点 ,且与直线
,且与直线 垂直,则直线
垂直,则直线 的前10项和为30,则
的前10项和为30,则 ___________.
___________. 值是___________.
值是___________.
 为常数,函数
为常数,函数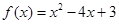 ,若
,若 在
在 上是增函数,则
上是增函数,则 被圆
被圆 所截得的线段长为________.
所截得的线段长为________. 是双曲线
是双曲线 上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.
上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.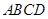 中,若
中,若 ,则
,则 ________.
________. 是球面上三点,且
是球面上三点,且 ,若球心
,若球心 到平面
到平面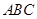 的距离为
的距离为 ,则该球的表面积为__________
,则该球的表面积为__________ .
. 中,
中, ,则
,则 的值为___________.
的值为___________.

 且
且 ,则
,则 ___________.
___________.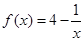 ,若存在区间
,若存在区间 ,使得
,使得 ,则实数
,则实数 的取值范围是___________.
的取值范围是___________. ,且
,且 ,则
,则 的值为
的值为

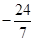

 的反函数是
的反函数是

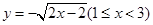

 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是



 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时, ;当
;当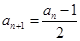 .
. 成等差数列,求
成等差数列,求 (
( 且
且 N),数列
N),数列 ,求证:
,求证: ;
; (
( N)时,都有
N)时,都有 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号