北京市西城区高二下学期期末考试理科数学试卷
已知从A口袋中摸出一个球是红球的概率为 ,从B口袋中摸出一个球是红球的概率为
,从B口袋中摸出一个球是红球的概率为 。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
A. |
B. |
C. |
D. |
从0,1,2,3中选取三个不同的数字组成一个三位数,则不同的三位数有( )
| A.24个 | B.20个 | C.18个 | D.15个 |
如果用反证法证明“数列 的各项均小于2”,那么应假设( )
的各项均小于2”,那么应假设( )
A.数列 的各项均大于2 的各项均大于2 |
B.数列 的各项均大于或等于2 的各项均大于或等于2 |
C.数列 中存在一项 中存在一项 |
D.数列 中存在一项 中存在一项 , , |
已知100件产品中有97件正品和3件次品,现从中任意抽出3件产品进行检查,则恰好抽出2件次品的抽法种数是( )
A. |
B. |
C. |
D. |
若5个人站成一排,且要求甲必须站在乙、丙两人之间,则不同的排法有( )
| A.80种 | B.40种 | C.36种 | D.20种 |
函数 的图象如图所示,且
的图象如图所示,且 在
在 与
与 处取得极值,给出下列判断:
处取得极值,给出下列判断:
① ;
;
② ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
已知某一随机变量X的分布列如下:
| X |
3 |
b |
8 |
| P |
0.2 |
0.5 |
a |
且 ,则a=__________;b=__________。
,则a=__________;b=__________。
二项式 的展开式中,常数项等于__________;二项式系数和为__________。
的展开式中,常数项等于__________;二项式系数和为__________。
抛掷一个骰子,若掷出5点或6点就说试验成功,则在3次试验中恰有2次成功的概率为__________。
已知函数 ,且
,且 是函数
是函数 的极值点。给出以下几个问题:
的极值点。给出以下几个问题:
① ;②
;② ;③
;③ ;④
;④
其中正确的命题是__________。(填出所有正确命题的序号)
已知数列 中,
中, ,其中
,其中 。
。
(1)计算 的值;
的值;
(2)根据计算结果猜想 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
某企业主要生产甲、乙两种品牌的空调,由于受到空调在保修期内维修费等因素的影响,企业生产每台空调的利润与该空调首次出现故障的时间有关,甲、乙两种品牌空调的保修期均为3年,现从该厂已售出的两种品牌空调中各随机抽取50台,统计数据如下:
| 品牌 |
甲 |
乙 |
|||||
| 首次出现故障时间 x年 |
 |
 |
 |
 |
 |
 |
 |
| 空调数量(台) |
1 |
2 |
4 |
43 |
2 |
3 |
45 |
| 每台利润(千元) |
1 |
2 |
2.5 |
2.7 |
1.5 |
2.6 |
2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌空调中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的空调均能售出,记生产一台甲品牌空调的利润为X1,生产一台乙品牌空调的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌空调销量相当,但由于资金限制,只能生产其中一种品牌空调,若从经济效益的角度考虑,你认为应该生产哪种品牌的空调?说明理由。
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望。
的分布列和数学期望。
已知函数 。
。
(1)当 时,求
时,求 的单调区间、最大值;
的单调区间、最大值;
(2)设函数 ,若存在实数
,若存在实数 使得
使得 ,求m的取值范围。
,求m的取值范围。
 等于( )
等于( )



 =( )
=( ) =( )
=( ) 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )


 ,则
,则 =____________。
=____________。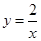 在点(1,2)处切线的斜率为__________。
在点(1,2)处切线的斜率为__________。 ,其中
,其中 。
。 ,求函数
,求函数 的极值点和极值;
的极值点和极值; 上的最小值。
上的最小值。 ,设曲线
,设曲线 在点
在点 处的切线为
处的切线为 。
。 的值;
的值; ,其中
,其中 。
。 时,
时, 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号