高中数学随机思想的发展试题

设随机变量ξ的概率分布列为，，则　　　　.

随机变量服从二项分布～，且则等于（   ）

A．

B．

C．1

D．0

现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.
（Ⅰ）求这4个人中恰有2人去参加甲游戏的概率；
（Ⅱ）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；
（Ⅲ）用 $X,Y$分别表示这4个人中去参加甲、乙游戏的人数，记 $\xi =\left|X-Y\right|$，求随机变量 $\xi$的分布列与数学期望 $E\xi$.

根据以往的经验，某工程施工期间的降水量 $X$（单位： $mm$）对工期的影响如下表：

降水量 $X$	$X<300$	$300\le X<700$	$700\le X<900$	$X\ge 900$
工期延误天数 $Y$	0	2	6	10

历年气象资料表明，该工程施工期间降水量 $X$小于300，700，900的概率分别为0.3，0.7，0.9. 求：
（Ⅰ）工期延误天数 $Y$的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率.

某银行柜台设有一个服务窗口，假设顾客办理业务所需的时间互相独立，且都是整数分钟，对以往顾客办理业务所需的时间统计结果如下：

从第一个顾客开始办理业务时计时.
（1）估计第三个顾客恰好等待4分钟开始办理业务的概率；
（2） $X$表示至第2分钟末已办理完业务的顾客人数，求 $X$的分布列及数学期望.

随机变量X的分布列如下表，且E(X)＝1.1，则D(X)＝________.

X	0	1	x
P		p

设服从二项分布B（n，p）的随机变量ξ的期望和方差分别是2.4与1.44，则二项分布的参数n、p的值为（   ）

A．n=4，p=0.6	B．n=6，p=0.4
C．n=8，p=0.3	D．n=24，p=0.1

(用数字表示结果)
某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选一题答一题的方式进行。每位选手最多有5次答题机会。选手累计答对3题或答错三题终止初赛的比赛。答对三题直接进入决赛，答错3题则被淘汰。已知选手甲连续两次答错的概率为(已知甲回答每个问题的正确率相同，并且相互之间没有影响)
(1)求选手甲回答一个问题的正确率；
(2)求选手甲进入决赛的概率；
(3)设选手甲在初赛中答题个数为X，试写出X的分布列，并求甲在初赛中平均答题个数。

某学校设计了一个实验学科的考查方案：考生从6道备选题中一次性抽取3道题，规定至少正确完成其中2道题便可通过，已知6道备选题中考生甲有4道能正确完成，2道不能完成；考生乙正确完成每道题的概率都是，且每题正确完成与否互不影响．
⑴求甲正确完成的题数的分布列及期望；求乙正确完成的题数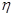的分布列及期望；
⑵请用统计知识分析比较两名考生这门学科的水平．

某保险公司新开设了一项保险业务，若在一年内事件E发生，该公司要赔偿元．设在一年内发生的概率为1%，为使公司收益的期望值等于的百分之十，公司应要求顾客交保险金为  
元．（用含的代数式表示）

随机变量的分布如图所示则数学期望         ．

	0	1	2	3

 

某学校要从5名男生和2名女生中选出2人作为志愿者，若用随机变量表示选出的志愿者中女生的人数，则数学期望=____________.（结果用最简分数表示）

学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有2人，会跳舞的有5人，现从中选2人．设为选出的人中既会唱歌又会跳舞的人数，且．
（1）求文娱队的队员人数；
（2）写出的概率分布列并计算

有一种舞台灯，外形是正六棱柱，在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用表示更换的面数，用表示更换费用。
(1)求①号面需要更换的概率；    
(2)求6个面中恰好有2个面需要更换的概率；
(3)写出的分布列，求的数学期望。

已知二项分布满足X～B（3，），则(X=2)=   ▲   ．（用分数表示）