(用数字表示结果)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选一题答一题的方式进行。每位选手最多有5次答题机会。选手累计答对3题或答错三题终止初赛的比赛。答对三题直接进入决赛,答错3题则被淘汰。已知选手甲连续两次答错的概率为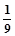 (已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(1)求选手甲回答一个问题的正确率;
(2)求选手甲进入决赛的概率;
(3)设选手甲在初赛中答题个数为X,试写出X的分布列,并求甲在初赛中平均答题个数。
相关知识点
推荐套卷
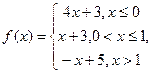 的最大值.
的最大值.
 )已知
)已知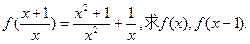

 试分别求出系统甲、乙能正常工作的概率p1,p2;
试分别求出系统甲、乙能正常工作的概率p1,p2;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号