[江苏]2012届江苏省南通市通州区高三4月查漏补缺专项检测数学试卷
空间三条直线中,任何两条不共面,且两两互相垂直,另一条直线 与这三条直线所成的角均为
与这三条直线所成的角均为 ,则
,则 .
.
将一个长和宽分别为 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .
已知函数 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图象关于
的图象关于 对称.若对任意的
对称.若对任意的 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的取值范围是 .
的取值范围是 .
设函数 ,其中
,其中 ,若
,若 ,且图象的一条对称轴离一个对称中心的最近距离是
,且图象的一条对称轴离一个对称中心的最近距离是 .
.
(1)求函数 的解析式;
的解析式;
(2)若 是
是 的三个内角,且
的三个内角,且 ,求
,求 的取值范围
的取值范围
在所有棱长都相等的斜三棱柱 中,已知
中,已知 ,
, ,且
,且 ,连接
,连接 .
.
(1)求证: 平面
平面 ;
;
(2)求证:四边形 为正方形.
为正方形.
如图1, 、
、 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段 和曲线段
和曲线段 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥 上某点
上某点 分别修建与
分别修建与 、
、 平行的栈桥
平行的栈桥 、
、 ,且以
,且以 、
、 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段 的方程是
的方程是
 ,曲线段
,曲线段 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为 ,记
,记 (题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(1)求 的取值范围;
的取值范围;
(2)试写出三角形观光平台 面积
面积 关于
关于 的函数解析式,并求出该面积的最小值.
的函数解析式,并求出该面积的最小值.
已知椭圆 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 第一象限内),过点
第一象限内),过点 作圆
作圆 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、 .
.
(1)证明: ;
;
(2)若椭圆离心率为 ,求线段
,求线段 长度的最大值.
长度的最大值.
已知数列 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数 ,若任意的
,若任意的 ,
, (
( ≤
≤ ≤
≤ ≤
≤ ),
), 仍是
仍是 中的项,则称数列
中的项,则称数列 为“
为“ 项可减数列”.
项可减数列”.
(1)已知数列 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列 是“
是“ 项可减数
项可减数
列”,试确定 的最大值;
的最大值;
(2)求证:若数列 是“
是“ 项可减数列”,则其前
项可减数列”,则其前 项的和
项的和 ;
;
(3)已知 是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
并说明理由.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的 点为极点,
点为极点, 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求直线 的倾斜角;
的倾斜角;
(2)若直线 与曲线
与曲线 交于
交于 两点,求
两点,求
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.
(1)求文娱队的队员人数;
(2)写出 的概率分布列并计算
的概率分布列并计算
 满足
满足 (
( 是虚数单位),则
是虚数单位),则 .
. ,集合
,集合 ,
, ,则
,则 中最大的元素是 .
中最大的元素是 . 与直线
与直线 平行的充要条件是 .
平行的充要条件是 . 的前
的前 项和为
项和为 ,若
,若 ,则数列
,则数列 是 .
是 . 往
往 走,且只能向右或向下走,随机地选一种走法,则经过点
走,且只能向右或向下走,随机地选一种走法,则经过点 的概率是 .
的概率是 .
 满足
满足 ,则
,则 的值为 .
的值为 . 有且仅有一个公共点,并且过点
有且仅有一个公共点,并且过点 的直线方程为 .
的直线方程为 .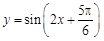 的图象向左平移至少 个单位,可得一个偶函数的图象.
的图象向左平移至少 个单位,可得一个偶函数的图象. 中,角
中,角 所对边分别是
所对边分别是 ,若
,若 ,则
,则 .
. 中,
中, ,
, 为
为 在
在 ,且
,且 ,则边
,则边 上的高
上的高 的最大值为 .
的最大值为 . ,其前
,其前 项的和为
项的和为 ,且
,且 ,若
,若 ,且数列
,且数列 的前
的前 ,则
,则 .
. (
( ).
). ,
, 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围; ,求方程
,求方程 在
在 上解的个数.
上解的个数. ,向量
,向量 .求向量
.求向量 ,使得
,使得 .
. 和
和 中,
中, ,
, ,
, ,其中
,其中 且
且 ,
, .设
.设 ,
, ,试问在区间
,试问在区间 上是否存在实数
上是否存在实数 使得
使得 .若存在,求出
.若存在,求出 ;若不存在,试说明理由.
;若不存在,试说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号