高中数学正交试验设计方法试题

某地举行篮球比赛，其中男子篮球总决赛在雄风队与豪杰队之间角逐，采用七局四胜制，若有一队胜4场，由此队获胜且结束比赛，因而队实力非常接近，在每场比赛中两队获胜是等可能的。据以往资料统计，每场比赛组织者可获门票收入5万元，两队决出胜负后，问：
（1）求组织者在此次决赛中获门票收入为20万元的概率。
（2）求组织者在此次决赛中获门票收入不少于30万元的概率。
（1）门票收入20万无，必须比赛四场，且能决出胜负

某车间在三天内，每天生产10件某产品，其中第一天，第二天分别生产出了1件、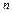件次品，而质检部每天要从生产的10件产品中随意抽取4件进行检查，若发现有次品，则当天的产品不能通过。则第一天通过检查的概率      ；  若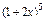的第三项的二项式系数为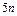，则第二天通过检查的概率       

.在集合内任取一个元素，能使代数式的概率是多少？

某人射击一次击中目标的概率为0.6，经过3次射击，此人至少有2次击中目标的概率为：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 　）

一场篮球比赛到了最后5分钟，甲队比乙队少得5分。如果甲队全投3分球，则有8次投篮机会。如果甲队全投2分球，则有3次投篮机会。假设甲队队员投3分球的命中率均为0.6，投2分球的命中率均为0 .8，并且甲队加强防守，不给乙队投篮机会．问全投3分球与全投2分球这两种方案中选择哪一种甲队获胜的概率较大？

某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）．
(１)求至少3人同时上网的概率；
(２)至少几人同时上网的概率小于0.3？

甲、乙两颗卫星同时监测台风，根据长期经验得知，甲、乙预报台风准确的概率分别为0.8和0.75.求：(1) 在同一次预报中，甲、乙两卫星只有一颗预报准确的概率；(2) 若甲独立预报4次，至少有3次预报准确的概率.

某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试，
面试合格者可以正式签约，毕业生甲表示只要面试合格就签约，毕业生乙和丙则约定：两人
面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是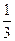，且面试是否合
格互不影响，求：（I）至少有1人面试合格的概率；（II）签约人数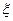的分布列和数学期望。

甲乙两个射手，甲击中靶心的概率为P，乙击中靶心的概率为，每次射击互相不受影响，且甲射击两次均未命中靶心的概率为。 （1）求甲击中靶心的概率P； （2）求乙射击两次至少命中一次的概率； （3）若甲、乙二人各射击2次，求两人共命中2次的概率。

假设每一架飞机的引擎在飞行中出现故障的概率为1-P，且各引擎是否出故障是独立的，已知4引擎飞机中至少有3个引擎正常运行，飞机就能成功运行；2引擎飞机中要2个引擎全部正常运行，飞机才能成功运行.要使4引擎飞机比2引擎飞机更安全，则P的取值范围？

有10道单项选择题，每题有4个选项。某人随机选其中一个答案（每个选项被选出的可能性相同），求答对多少题的概率最大？并求出此种情况下概率的大小.（保留两位有效数字）

10个球中,有4个红球和6个白球,每次从中取一个球,然后放回,连续取4次,恰有1个红球的概率为          .

（本小题满分12分）已知高二年级的某6名学生，独立回答某类问题时答对的概率都是0.5，而将这6名同学平均分为甲、乙、丙3个小组后，每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7，若各个同学或各个小组回答问题时都是相互独立的．
（Ⅰ）这6名同学平均分成3组，共有分法多少种？
（Ⅱ）若分组后，3个小组中恰有2组能答对此类问题的概率是多少？
（Ⅲ）若要求独立回答，则这6名学生中至多有4人能答对此类问题的概率是多少？

（本小题满分12分）抛一枚均匀的骰子（骰子的六面分别有数字1、2、3、4、5、6）来构造数列
（1）求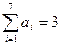的概率；（2）若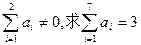的概率.

某地区试行高考考试改革：在高三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是，每次测试通过与否互相独立. 规定：若前4次都没有通过测试，则第5次不能参加测试．（1）求该学生恰好经过4次测试考上大学的概率；（2）求该学生考上大学的概率．