（本小题满分12分）已知高二年级的某6名学生，独立回答某类问题时答对的概率都是0.5，而将这6名同学平均分为甲、乙、丙3个小组后，每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7，若各个同学或各个小组回答问题时都是相互独立的．
（Ⅰ）这6名同学平均分成3组，共有分法多少种？
（Ⅱ）若分组后，3个小组中恰有2组能答对此类问题的概率是多少？
（Ⅲ）若要求独立回答，则这6名学生中至多有4人能答对此类问题的概率是多少？
相关试题
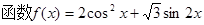
的最小正周期和单调递
增区间
(14分)设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3∶1，在满足条件①、②的所有圆中，求圆心到直线l:x-2y=0的距离最小的圆的方程。
(12分)已知曲线C：x2+y2-2x-4y+m=0
（1）当m为何值时，曲线C表示圆；
（2）若曲线C与直线x+2y-4=0交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值。
。
相关知识点
推荐套卷
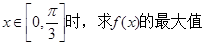
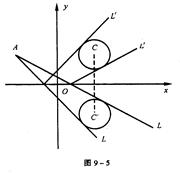
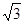粤公网安备 44130202000953号