(12分)如图7-4,已知△ABC中, ∠ACB=90°,CD⊥AB,且AD=1,BD=2,△ACD绕CD旋转至A′CD,使点A′与点B之间的距离A′B=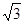 。
。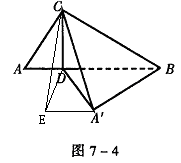
(1)求证:BA′⊥平面A′CD;
(2)求二面角A′-CD-B的大小;
(3)求异面直线A′C与BD所成的角的余弦值。
推荐套卷
(12分)如图7-4,已知△ABC中, ∠ACB=90°,CD⊥AB,且AD=1,BD=2,△ACD绕CD旋转至A′CD,使点A′与点B之间的距离A′B=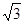 。
。
(1)求证:BA′⊥平面A′CD;
(2)求二面角A′-CD-B的大小;
(3)求异面直线A′C与BD所成的角的余弦值。