设随机变量 的概率分布列为
的概率分布列为

则 ( )
( )
A. |
B. |
C. |
D. |
实验女排和育才女排两队进行比赛,在一局比赛中实验女排获胜的概率是2/3,没有平局.若采用三局两胜制,即先胜两局者获胜且比赛结束,则实验女排获胜的概率等于
A. |
B. |
C. |
D. |
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
| |
认为作业多 |
认为作业不多 |
总数 |
| 喜欢玩电脑游戏 |
18 |
9 |
27 |
| 不喜欢玩电脑游戏 |
8 |
15 |
23 |
| 总数 |
26 |
24 |
50 |
根据表中数据得到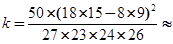 5.059,因为p(K
5.059,因为p(K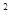 ≥5.024)=0.025,
≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
(A)97.5% (B) 95% (C)90% (D)无充分根据
某校150名教职工中,有老年人20个,中年人50个,青年人80个,从中抽取20个作为样本.
①采用随机抽样法:抽签取出30个样本;
②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本;
③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本.
下列说法中正确的是( )
| A.无论采用哪种方法,这150个教工中每一个被抽到的概率都相等 |
| B.①②两种抽样方法,这150个教工中每一个被抽到的概率都相等;③并非如此 |
| C.①③两种抽样方法,这150个教工中每一个被抽到的概率都相等;②并非如此 |
| D.采用不同的抽样方法,这150个教工中每一个被抽到的概率是各不相同的 |
甲乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为 ,则甲以
,则甲以 的比分获胜的概率为( )
的比分获胜的概率为( )
A. |
B. |
C. |
D. |
设X为随机变量,X~B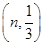 ,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
A.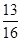 |
B.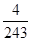 |
C.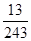 |
D.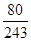 |
如图;现有一迷失方向的小青蛙在3处,它每跳动一次可以等机会地进入相邻的任意一格(如若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入l,2,4,5处),则它在第三次跳动后,进入5处的概率是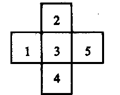
A.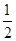 |
B.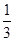 |
C.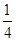 |
D.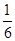 |
箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是
A. |
B. |
C. |
D. |
箱中有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中重新取球,若取出白球,则停止取球,那么在第四次取球之后停止的概率为( )
A.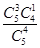 |
B.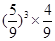 |
C.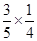 |
D.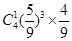 |
口袋内放有大小相同的2个红球和1个白球,有放回地每次摸取一个球,定义数列{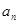 }为
}为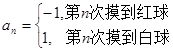 .如果
.如果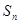 为数列{
为数列{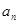 }的前
}的前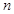 项和,那么
项和,那么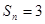 的概率为 ( )
的概率为 ( )
A.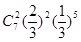 |
B. |
C.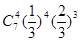 |
D.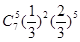 |