高考数学(文)二轮专题复习与测试专题6第2课时练习卷
投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一个发生的概率是( )
A. |
B. |
C. |
D. |
设X为随机变量,X~B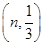 ,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
A.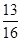 |
B.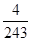 |
C.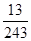 |
D.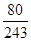 |
有一底面半径为1,高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为( )
A. |
B. |
C. |
D. |
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,则从2号箱取出红球的概率是( )
A. |
B. |
C. |
D. |
签盒中有编号为1、2、3、4、5、6的六支签,从中任意取3支,设X为这3支签的号码之中最大的一个,则X的数学期望为( )
| A.5 | B.5.25 | C.5.8 | D.4.6 |
在区间[-2,4]上随机地取一个数x,若x满足|x|≤m的概率为 ,则m=________.
,则m=________.
某项游戏活动的奖励分成一、二、三等奖且相应获奖概率是以a1为首项,公比为2的等比数列,相应资金是以700元为首项,公差为-140元的等差数列,则参与该游戏获得资金的期望为________元.
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为 ,乙投进的概率为
,乙投进的概率为 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
甲、乙等五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列及数学期望.
气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t(单位:℃) |
t≤22 |
22<t≤28 |
28<t≤32 |
t>32 |
| 天数 |
6 |
12 |
Y |
Z |
由于工作疏忽,统计表被墨水污染,Y和Z数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
某水果商根据多年的销售经验,六月份的日最高气温t(单位:℃)对西瓜的销售影响如下表:
| 日最高气温t(单位:℃) |
t≤22 |
22<t≤28 |
28<t≤32 |
t>32 |
| 日销售额X(单位:千元) |
2 |
5 |
6 |
8 |
(1)求Y,Z的值;
(2)若视频率为概率,求六月份西瓜日销售额的期望和方差;
(3)在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号