甲乙两人各有相同的小球10个,在每人的10个小球 中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
某装置由两套系统M,N组成,只要有一套系统工作正常,该 装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是
装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是 ,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
(I )分别求系统M,N正常工作的概率 ;
;
(II)设该装I中两套系统正常工作的套数为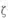 ,求
,求 的分布列和期望.
的分布列和期望.
一次测量中出现正误差和负误差的概率都是 ,则在5次测量中,恰好出现3次正误差的概率是
,则在5次测量中,恰好出现3次正误差的概率是
A. |
B. |
C. |
D. |
(本题12分)已知某种从太空带回的植物种子每粒成功发芽的概率都为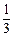 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求实验成功的平均次数;
(2) 第二小组连续进行实验,求实验首次成功时所需的实验次数的期望;
(3)两个小组分别进行2次试验,求至少有2次实验成功的概率.
已知某位射手每次击中目标的概率为0.8,每次射击的结果相互独立,那么他在6次射击中,最有可能击中目标的次数为_________次.
某批产品的次品率为 ,现在从10件产品中任意的依次抽取3件,分别以放回和不放回的方式抽取,则恰有一件次品的概率分别为( )
,现在从10件产品中任意的依次抽取3件,分别以放回和不放回的方式抽取,则恰有一件次品的概率分别为( )
A. |
B. |
C. |
D. |
某射手射击1次,击中目标的概率是0.9 .她连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是 ;③他至少击中目标1次的概率是
;③他至少击中目标1次的概率是 .其中正确结论的序号是 _____(写出所有正确结论的序号).
.其中正确结论的序号是 _____(写出所有正确结论的序号). 14
14
在4次独立试验中,事件A出现的概率相同,若事件A至少发生1次的概率是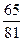 ,则事件A 在一次试验中出现的概率是( )
,则事件A 在一次试验中出现的概率是( ) 12
12
A.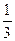 |
B.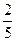 |
C.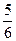 |
D. |