湖北省三峡高中高二下学期期末考试(理科)数学卷
把一枚质地不均匀的硬币连掷5次,若恰有一次正面向上的概率和恰有两次正面向上的概率相同(均不为0也不为1),则恰有三次正面向上的概率是
A. |
B. |
C. |
D. |
设有甲、乙两把不相同的锁,甲锁配有2把钥匙,乙锁配有2把钥匙,这4把钥匙与不能开这两把锁的2把钥匙混在一起,从中任取2把钥匙能打开2把锁的概率是
A. |
B. |
C. |
D. |
已知命题“若函数 在
在 是增函数,则
是增函数,则 ”,则下列结论正确的是
”,则下列结论正确的是
A.否命题是“若函数 在 在 是减函数,则 是减函数,则 ”,是真命题 ”,是真命题 |
B.逆命题是“若 ,则函数 ,则函数 在 在 是增函数”, 是假命题 是增函数”, 是假命题 |
C.逆否命题是“若 ,则函数 ,则函数 在 在 是减函数”, 是真命题 是减函数”, 是真命题 |
D.逆否命题是“若 ,则函数 ,则函数 在 在 不是增函数”, 是真命题 不是增函数”, 是真命题 |
某厂生产的一种饮料每瓶售价2元,销售中规定5个空瓶子可换取一瓶饮料,该种饮料每瓶成本1元,那么该种饮料每瓶利润应是
| A.0.55元 | B.0.60元 | C.0.66元 | D.1元 |
路灯距地面为 米,一个身高为
米,一个身高为 米的人以每秒
米的人以每秒 米的速度匀速地从路灯的正下方沿某直线离开路灯,那么人影长度的变化率为 米/秒(精确到
米的速度匀速地从路灯的正下方沿某直线离开路灯,那么人影长度的变化率为 米/秒(精确到 );
);
某中学高二年级理科共有学生600人,一次数学考试的成绩(试卷满分150分)服从正态分布N(100,δ2),统计结果显示学生考试成绩在80分到100分之间的人数约占总人数的 ,则此次考试成绩不低于120分的学生约有 人;
,则此次考试成绩不低于120分的学生约有 人;
某机关有老、中、青人数分别为18、12、6,现从中抽取一个容量为X的样本,如果采用系统抽样和分层抽样,则不用剔除个体,如果容量增加1个,则在采用系统抽样时,需要在总体中剔除1个个体,则样本容量X=________;
甲、乙两厂生产同一种商品,甲厂生产的此商品占市场上的 ,乙厂生产的此商品占市场上的
,乙厂生产的此商品占市场上的 ;甲厂商品的合格率为
;甲厂商品的合格率为 ,乙厂商品的合格率为
,乙厂商品的合格率为 。若某人购买了此商品发现为次品,则此次品为甲厂生产的概率为 (用最简分数表示)。
。若某人购买了此商品发现为次品,则此次品为甲厂生产的概率为 (用最简分数表示)。
(本题12分)已知某种从太空带回的植物种子每粒成功发芽的概率都为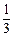 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求实验成功的平均次数;
(2) 第二小组连续进行实验,求实验首次成功时所需的实验次数的期望;
(3)两个小组分别进行2次试验,求至少有2次实验成功的概率.
(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间 ,
, ,
, ,
, ,
, ,
, 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
(本题12分)某鲜花店每天以每束2.5元购入新鲜玫瑰花并以每束5元的价格销售,店主根据以往的销售统计得到每天能以此价格售出的玫瑰花数 的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
的分布列如表所示。若某天所购进的玫瑰花未售完,则当天未售出的玫瑰花将以每束1.5元的价格降价处理完毕。
 |
30 |
40 |
50 |
| P |
 |
 |
 |
(1)若某天店主购入玫瑰花40束,试求该天从玫瑰花销售中所获利润的期望;
(2)店主每天玫瑰花的进货量
 ,单位:束
,单位:束 为多少时,其有望从玫瑰花销售中获得最大利润?
为多少时,其有望从玫瑰花销售中获得最大利润?
(本题13分)已知函数
(1)已知一直线 经过原点
经过原点 且与曲线
且与曲线 相切,求
相切,求 的直线方程;
的直线方程;
(2)若关于 的方程
的方程 有两个不等的实根,求实数
有两个不等的实根,求实数 的取值范围。
的取值范围。
 为全集,
为全集, 是
是 ,则集合
,则集合




 的方程
的方程 有实根
有实根 ,复数
,复数 ,则复数
,则复数 在复平面内的对应点到原点的距离为
在复平面内的对应点到原点的距离为
 在点
在点 处连续,则常数
处连续,则常数 的值是
的值是 ∽
∽ ∽
∽ ,记
,记 ,则
,则


 的大小关系不定
的大小关系不定 是定义在
是定义在 的可导函数,对
的可导函数,对 ,都有
,都有 ,且
,且 ,则
,则


 在R上满足
在R上满足 ,则曲线
,则曲线 在点
在点 处的切线方程是
处的切线方程是



 ,集合
,集合 ,则
,则 ;
; ,已知
,已知 在
在 上有最小值3。
上有最小值3。
 时,求
时,求 在
在 处的切线方程;
处的切线方程; 时,求
时,求 的极值;
的极值; 时,求
时,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号