如图, 中,
中, 是
是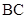 的中点,
的中点, ,
, .将
.将 沿
沿 折起,使
折起,使 点与图中
点与图中 点重合.
点重合.
(1)求证: 平面
平面 ;
;
(2)当三棱锥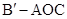 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(3)在(2)条件下,试问在线段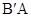 上是否存在一点
上是否存在一点 ,使
,使 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?证明你的结论.
?证明你的结论.
设 表示不同的直线,
表示不同的直线, 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题:
①若 ,且
,且 ,则
,则 ;
;
②若 ,且
,且 ,则
,则 ;
;
③若 ,
, ,
, ,则
,则 ;
;
④若 ,
, ,
, 且
且 ,则
,则 .
.
其中正确命题的个数是()
| A.1 | B.2 | C.3 | D.4 |
在如图所示的几何体中, △ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F为BE的中点.
(Ⅰ)求证:平面DBE⊥平面ABE;
(Ⅱ)求直线BD和平面ACDE所成角的余弦值.
(本小题满分12分)
如图,已知正三棱柱 各棱长都是4,
各棱长都是4, 是
是 的中点,动点
的中点,动点 在侧棱
在侧棱 上,且不与点
上,且不与点 重合.
重合.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)设二面角 的大小为
的大小为 ,求
,求 的最小值.
的最小值.
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.
(1)证明: ;
;
(2)是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?
?
若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
如图,在多面体 中,正方形
中,正方形 与梯形
与梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, ,
, ,
, ,
, 分别为
分别为 和
和 的中点.
的中点.
(1)求证: 平面
平面
(2)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
如图,矩形 中,
中,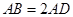 ,
, 为边
为边 的中点,将
的中点,将 沿直线
沿直线 翻折成
翻折成 ,若
,若 为线段
为线段 的中点,则在
的中点,则在 翻折过程中,下面四个选项中正确的是 (填写所有的正确选项)
翻折过程中,下面四个选项中正确的是 (填写所有的正确选项)
(1) 是定值
是定值
(2)点 在某个球面上运动
在某个球面上运动
(3)存在某个位置,使
(4)存在某个位置,使 平面
平面
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,则下面四个命题中错误的是().
是两个不同的平面,则下面四个命题中错误的是().
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 或 或 |
D.若 , , ,则 ,则 |