已知空间直角坐标系o﹣xyz中的点A的坐标为(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点,则点P的坐标满足的条件是 .
在梯形ABCD中,AB∥CD,AB 平面α,CD
平面α,CD 平面α,则直线CD与平面α内的直线的位置关系可能是________.
平面α,则直线CD与平面α内的直线的位置关系可能是________.
对于四面体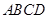 ,以下说法中,正确的序号为 (多选、少选、选错均不得分).
,以下说法中,正确的序号为 (多选、少选、选错均不得分).
①若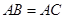 ,
,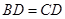 ,
,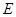 为
为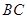 中点,则平面
中点,则平面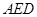 ⊥平面
⊥平面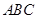 ;
;
②若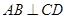 ,
, ,则
,则 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以 为端点的三条棱所在直线两两垂直,则
为端点的三条棱所在直线两两垂直,则 在平面
在平面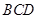 内的射影为
内的射影为 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
给出四个命题:
①平行于同一平面的两个不重合的平面平行;
②平行于同一直线的两个不重合的平面平行;
③垂直于同一平面的两个不重合的平面平行;
④垂直于同一直线的两个不重合的平面平行;
其中真命题的序号是________.
三棱锥 中,
中, 若
若 ,
, 是该三棱锥外部(不含表面)的一点,给出下列四个命题,
是该三棱锥外部(不含表面)的一点,给出下列四个命题,
① 存在无数个点 ,使
,使 ;
;
② 存在唯一点 ,使四面体
,使四面体 为正三棱锥;
为正三棱锥;
③ 存在无数个点 ,使
,使 ;
;
④ 存在唯一点 ,使四面体
,使四面体 有三个面为直角三角形.
有三个面为直角三角形.
其中正确命题的序号是 .
设l,m是不同的直线,α,β,γ是不同的平面,则下列命题正确的是______________.
①若l⊥m,m⊥α,则l⊥α或 l∥α
②若l⊥γ,α⊥γ,则l∥α或 l α
α
③若l∥α,m∥α,则l∥m或 l与m相交
④若l∥α,α⊥β,则l⊥β或l β
β
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,
① 平面
平面 ;
;
② 平面
平面 ;
;
③CN与BM成 角;
角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。 (写出所有正确命题的序号)
在正方体 中,点
中,点 为正方形
为正方形 的中心.下列说法正确的是 (写出你认为正确的所有命题的序号).
的中心.下列说法正确的是 (写出你认为正确的所有命题的序号).
①直线 与平面
与平面 所成角的正切值为
所成角的正切值为 ;
;
②若 ,
, 分别是正方形
分别是正方形 ,
, 的中心,则
的中心,则 ;
;
③若 ,
, 分别是正方形
分别是正方形 ,
, 的中心,则
的中心,则
 ;
;
④平面 中不存在使
中不存在使

 成立的
成立的 点.
点.
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点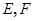 ,且
,且 ,则下列结论中正确的有 .(填写你认为正确的序号)
,则下列结论中正确的有 .(填写你认为正确的序号)

① ;
;
② ;
;
③若 为
为 上的一动点,则三棱锥
上的一动点,则三棱锥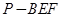 的体积为定值;
的体积为定值;
④在空间与直线 都相交的直线只有1条。
都相交的直线只有1条。
如图所示,在四边形 中,
中, ,将四边形
,将四边形 沿对角线
沿对角线 折成四面体
折成四面体 ,使平面
,使平面 平面
平面 ,则下列结论正确的是 .
,则下列结论正确的是 .

(1) ;
;
(2) ;
;
(3) 与平面
与平面 所成的角为
所成的角为 ;
;
(4)四面体 的体积为
的体积为 .
.
如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为 ,则
,则 的最大值为 .
的最大值为 .
