设 是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若 ,且
,且 ,则
,则 ”为真命题的是 . (填所正确条件的代号)
”为真命题的是 . (填所正确条件的代号)
① 为直线;
为直线;
② 为平面;
为平面;
③ 为直线,
为直线, 为平面;
为平面;
④ 为直线,
为直线, 为平面.
为平面.
已知 是直线,
是直线,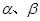 是平面,下列命题中:
是平面,下列命题中:
①若 垂直于
垂直于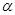 内两条直线,则
内两条直线,则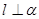 ;
;
②若 平行于
平行于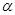 ,则
,则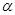 内可有无数条直线与
内可有无数条直线与 平行;
平行;
③若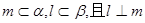 ,则
,则 ;
;
④若m⊥n,n⊥l则m∥l;
⑤若 ,则
,则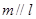 ;
;
正确的命题序号为__________.
设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的等价条件是
垂直的等价条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是 .(填写正确命题的序号)
①若m∥n,m⊥β,则 n⊥β;
②若m∥n,m∥β,则n∥β;
③若m∥α,m∥β,则α∥β;
④若n⊥α,n⊥β,则α⊥β.
设 为空间的两条直线,
为空间的两条直线, 为空间的两个平面,给出下列命题:
为空间的两个平面,给出下列命题:
①若

 ,
,

 , 则
, 则

 ;
;
②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
③若

 ,
,

 ,则
,则

 ;
;
④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则

 ;
;
上述命题中,其中假命题的序号是 .
a,b,c表示直线,M表示平面,给出下列四个命题:
①若a∥M,b∥M,则a∥b;
②若b M,a∥b,则a∥M;
M,a∥b,则a∥M;
③若a⊥c,b⊥c,则a∥b;
④若a⊥M,b⊥M,则a∥b.
⑤a⊥M,b M,若b∥M,则b⊥a
M,若b∥M,则b⊥a
其中正确命题的序号是 .
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,
① 平面
平面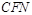 ;
;
② 平面
平面 ;
;
③CN与BM成 角;
角;
④DM与BN垂直.
⑤与该正方体各棱相切的球的表面积为 。
。
以上五个命题中,正确命题的序号是____ ____。
(写出所有正确命题的序号)
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题,其中所有正确命题的序号是___________.
①若m∥β,n∥β,m、n α,则α∥β .
α,则α∥β .
②若α⊥γ,β⊥γ,α∩β=m,n γ,则m⊥n .
γ,则m⊥n .
③若m⊥α,α⊥β,m∥n,则n∥β .
④若n∥α,n∥β,α∩β=m,那么m∥n .