已知 ,
, 是不重合的两条直线,
是不重合的两条直线, ,
, 是不重合的两个平面.下列命题:①若
是不重合的两个平面.下列命题:①若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;③若
;③若 ∥
∥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;④若
;④若 ∥
∥ ,
, ,则
,则 ∥
∥ .其中所有真命题的序号是 .
.其中所有真命题的序号是 .
设l,m是两条不同的直线,α是一个平面,则下列命题正确的个数为________.
①若l⊥m,m⊂α,则l⊥α;②若l⊥α,l∥m,则m⊥α;③若l∥α,m⊂α,则l∥m;④若l∥α,m∥α,则l∥m.
设、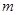 、
、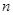 表示不同的直线,
表示不同的直线,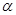 ,
,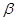 ,
, 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .
①若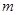 ∥
∥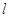 ,且
,且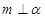 ,则
,则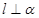 ;②若
;②若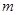 ∥
∥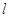 ,且
,且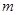 ∥
∥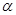 ,则
,则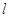 ∥
∥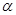 ;③若
;③若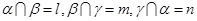 ,则
,则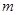 ∥
∥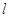 ∥
∥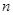 ;④若
;④若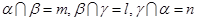 ,且
,且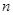 ∥
∥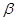 ,则
,则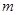 ∥
∥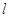 .
.
已知 ,
, 是不重合的两条直线,
是不重合的两条直线, ,
, 是不重合的两个平面.下列命题:①若
是不重合的两个平面.下列命题:①若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;③若
;③若 ∥
∥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;④若
;④若 ∥
∥ ,
, ,则
,则 ∥
∥ .其中所有真命题的序号是 .
.其中所有真命题的序号是 .
[2014·南通调研]设α,β是空间内两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题:________(用序号表示).
 是矩形,
是矩形, ,
, ,沿
,沿 将
将 折起到
折起到 ,使平面
,使平面 平面
平面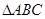 ,
, 是
是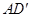 的中点,
的中点, 是
是 上的一点,给出下列结论:
上的一点,给出下列结论:
① 存在点 ,使得
,使得 平面
平面
② 存在点 ,使得
,使得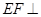 平面
平面
③ 存在点 ,使得
,使得 平面
平面
④ 存在点 ,使得
,使得 平面
平面
其中正确结论的序号是 .(写出所有正确结论的序号)
已知正三棱锥P-ABC,点P,A,B,C都在半径为 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为__________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为__________.
[2013·南京模拟]已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题:
①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;
②若l⊂α,l∥β,α∩β=m,则l∥m;
③若α∥β,l∥α,则l∥β;
④若l⊥α,m∥l,α∥β,则m⊥β.
其中真命题是________(写出所有真命题的序号).
在正方体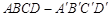 中,过对角线
中,过对角线 的一个平面交棱
的一个平面交棱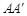 于E,交棱
于E,交棱 于F,则:①四边形
于F,则:①四边形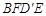 一定是平行四边形;②四边形
一定是平行四边形;②四边形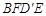 有可能是正方形;③四边形
有可能是正方形;③四边形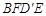 有可能是菱形;④四边形
有可能是菱形;④四边形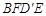 有可能垂直于平面
有可能垂直于平面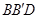 .
.
其中所有正确结论的序号是 .
(本小题满分12分)已知四棱锥 ,侧面
,侧面 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 为菱形,且
为菱形,且 .
.
(1)求证: ;
;
(2)求平面 与平面
与平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
如图所示,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确结论的序号是________.