已知直线 ,平面
,平面 ,且
,且 ,
, ,给出下列四个命题:
,给出下列四个命题:
①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;
;
③若 ,则
,则 ∥
∥ ;④若
;④若 ∥
∥ ,则
,则 ;
;
其中为真命题的序号是_______
设a、b为空间的两条直线,α、β为空间的两个平面,给出下列命题:
①若a∥α,a∥β,则α∥β;②若a⊥α,a⊥β,则α⊥β;
③若a∥α,b∥α,则a∥b;④若a⊥α,b⊥α,则a∥b.
上述命题中,所有真命题的序号是 .
如图所示,E、F分别是正方形SD1DD2的边D1D、DD2的中点沿SE,SF,EF将其折成一个几何体,使D1,D,D2重合,记作D。给出下列位置关系:①SD⊥面DEF; ②SE⊥面DEF; ③DF⊥SE; ④EF⊥面SED,其中成立的有 
已知直线 、
、 ,平面
,平面 、
、 ,给出下列命题:
,给出下列命题:
①若 ,且
,且 ,则
,则 ②若
②若 ,且
,且 ,则
,则
③若 ,且
,且 ,则
,则 ④若
④若 ,且
,且 ,则
,则
其中正确的命题的个数为 _ _.
已知正三棱柱P-ABC,点P,A,B,C都在半径为 的求面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为.
考察下列三个命题,在“________”都缺少同一个条件,补上这个条件使其构成真命题(其中 为不同直线,
为不同直线, 为不同平面),则此条件为______________.
为不同平面),则此条件为______________.
① ; ②
; ② ; ③
; ③
已知平面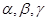 ,直线
,直线 满足:
满足: ,那么
,那么
①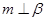 ; ②
; ②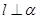 ; ③
; ③ ; ④
; ④ 。
。
可由上述条件可推出的结论有 ;
如图所示,AB是⊙O的直径, ⊙O,C为圆周上一点,若
⊙O,C为圆周上一点,若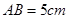 ,
, ,则B点到平面PAC的距离为 。
,则B点到平面PAC的距离为 。
给出下列四个命题:
①过平面外一点,作与该平面成 角的直线一定有无穷多条。
角的直线一定有无穷多条。
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为