已知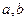 为直线,
为直线,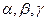 为平面,有下列三个命题:
为平面,有下列三个命题:
(1)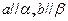 ,则
,则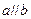 ;
;
(2)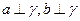 ,则
,则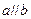 ;
;
(3)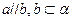 ,则
,则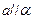 ;
;
(4)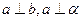 ,则
,则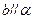 ;
;
其中正确命题是
如图甲,在△ABC中,AB⊥AC,AD⊥BC,
D是垂足,则AB2=BD·BC,该结论称为射
影定理。如图乙,在三棱锥A—BCD中,
AD⊥平面ABC,AO⊥平面BCD,O为垂
足,且O在△BCD内,类比射影定理,探
究S△BCO、S△BCD、S△ABC这三者之间满足的
关系式是 。
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如图所示五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是_____________. 
如右图,在直四棱柱A1B1C1D1-DABC中,当底面四边形ABCD满足条件______________时,有A1B⊥B1D1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形) 
知a,b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是______________.
①两条平行直线;
②两条互相垂直的直线;
③同一条直线;
④一条直线及其外一点.
在上面结论中,正确的编号是_________.(写出所有正确结论的编号)
在直四棱柱A1B1C1D1—ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形).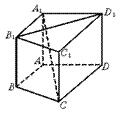
如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .