[江苏]2011-2012学年江苏省南京市东山外校高二下学期期中数学试卷
某地区打的士收费办法如下:不超过2公里 收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元,(其他因素不考虑)计算收费标准的框图如图所示, 则①处应填____________;
样本容量为10的一组数据,它们的平均数是5,频率条形图如图,则其标准差等于________(保留根号);
一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本,已知
B层中每个个体被抽到的概率都为 ,则总体中的个体数为__________;
,则总体中的个体数为__________;
先后抛掷两枚均匀的正方体骰子,骰子朝上的面的点数分别为x、y,则满足
的概率为________;
已知椭圆 的左右焦点分别为F1,F2,离心率为e,若椭圆上存在点P,使得
的左右焦点分别为F1,F2,离心率为e,若椭圆上存在点P,使得 ,则该离心率e的取值范围是__________;
,则该离心率e的取值范围是__________;
如图,已知正方形ABCD的边长为1,过正方形中心O 的直线MN分别交正方形的边AB,CD于点M,N,则当 取最小值时,
取最小值时, _________。
_________。
已知向量 =(
=( ,
, ),
), =(
=( ,
, ),定义函数
),定义函数 =
=
(1)求 的最小正周期
的最小正周期 ;
;
(2)若△ 的三边长
的三边长 成等比数列,且
成等比数列,且 ,求边
,求边 所对角
所对角 以及
以及 的大小。
的大小。
如图,在四棱锥 中,底面
中,底面 为矩形,平面
为矩形,平面 ⊥平面
⊥平面 ,
, ,
, ,
, 为
为 的中点,
的中点,
求证:(1) ∥平面
∥平面 ;(2)平面
;(2)平面 平面
平面 .
.
(本小题满分14分)
为了解学生升高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(Ⅰ)估计该校男生的人数;
(Ⅱ)估计该校学生身高在170~185cm之间的概率;
(Ⅲ)从样本中身高在165~180cm之间的女生中任选2人,求至少有1人身高在170~18cm之间的概率。
(本小题满分16分)
如图,椭圆 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,
,
(1)求到点 和直线
和直线 的距离相等的点
的距离相等的点 的轨迹方程。
的轨迹方程。
(2)过点 作直线交椭圆
作直线交椭圆 于点
于点 ,又直线
,又直线 交
交 于点
于点 ,若
,若 ,
,
求线段 的长;
的长;
(3)已知点 的坐标为
的坐标为 ,直线
,直线 交直线
交直线 于点
于点 ,且和椭圆
,且和椭圆 的一个交点为点
的一个交点为点 ,是否存在实数
,是否存在实数 ,使得
,使得 ,若存在,求出实数
,若存在,求出实数 ;若不存在,请说明理由。
;若不存在,请说明理由。
 是虚数单位,
是虚数单位, =___________;
=___________; 直线
直线 ,
, 相交,命题
相交,命题 直线
直线 是
是 的 条件;
的 条件;

 ,在定义域内任取一点
,在定义域内任取一点 ,使
,使 的概率是____;
的概率是____; 的一个焦点是
的一个焦点是 ,则
,则 ____________;
____________;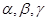 ,直线
,直线 满足:
满足: ,那么
,那么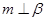 ; ②
; ②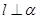 ; ③
; ③ ; ④
; ④ 。
。 的前n项和分别为
的前n项和分别为 和
和 ,若
,若 ,且
,且 是整数,则
是整数,则 的值为 ;
的值为 ; .
. 的方程
的方程 只有一个实数解,求实数
只有一个实数解,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号