(本小题满分16分)
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
(1)求 的长;
的长;
(2)求 的值;
的值;
(3)求证:A1B⊥C1M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2 ,PD=CD=2.
,PD=CD=2.
(1)求异面直线PA与BC所成角的正切值;
(2)证明平面PDC⊥平面ABCD;
(3)求直线PB与平面ABCD所成角的正弦值.
(本小题满分12分)如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)当二面角B—PC—D的大小为 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(本小题满分12分)如图,已知四棱锥 的底面为菱形,
的底面为菱形, ,
, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
(Ⅰ)求证:DE∥平面PAC.
(Ⅱ)求证:AB⊥PB;
(Ⅲ)若PC=BC,求二面角P—AB—C的大小.
(本小题满分12分)
如图,在三棱锥 中,面
中,面 面
面 ,
, 是正三角形,
是正三角形, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若异面直线 所成角的余弦值为
所成角的余弦值为 ,求二面角
,求二面角 的大小;
的大小;
(本小题满分9分)
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
(1)求证AC⊥BC1
(2)求证AC1∥平面CDB1
(本小题满分14分)如图,多面体ABCDEF中,平面ADEF⊥平面ABCD,正方形ADEF的边长为2,直角梯形ABCD中,AB∥CD,AD⊥DC,AB=2,CD=4. 
(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)试在平面CDE上确定点P,使点P到直线DC、DE的距离相等,且AP与平面BEF所成的角等于30°.
如图,已知菱形ACSB中,∠ABS=60°.沿着对角线SA将菱形ACSB折成三棱锥S﹣ABC,且在三棱锥S﹣ABC中,∠BAC=90°,O为BC中点.
(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求平面ASC与平面SCB夹角的余弦值.
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4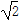 ,AB=2
,AB=2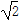 ,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
如图,在正方体 的棱长为
的棱长为 ,
, 为棱
为棱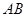 上的一动点.
上的一动点.

(1)若 为棱
为棱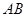 的中点,
的中点,
①求四棱锥 的体积
的体积
②求证:面 面
面
(2)若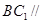 面
面 ,求证:
,求证: 为棱
为棱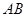 的中点.
的中点.
(本小题满分14分)如图,长方体ABCD—A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线 ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求三棱锥D—PAC的体积。