如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(Ⅰ)判定AE与PD是否垂直,并说明理由;
(Ⅱ)若PA=2,求二面角E-AF-C的余弦值.
一个几何体是由圆柱 和三棱锥
和三棱锥 组合而成,点A、B、C在圆柱上底面圆O的圆周上,
组合而成,点A、B、C在圆柱上底面圆O的圆周上, 平面
平面 ,
, ,
, ,其正视图、侧视图如图所示.
,其正视图、侧视图如图所示.
(1)求证: ;
;
(2)求锐二面角 的大小.
的大小.
如图,在平行四边形 中,
中, ,
, ,
, 为
为 的中点,将
的中点,将 沿直线
沿直线 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)证明:CE PD;
PD;
(2)设 、
、 分别为
分别为 、
、 的中点,求直线
的中点,求直线 与平面
与平面 所成的角.
所成的角.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.
(1)求证:PC //平面BDE;
(2)若PC⊥PA,PD=AD,求证:平面BDE⊥平面PAB.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是PB的中点,点F是EB的中点.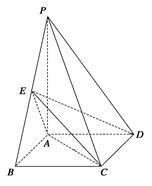
(Ⅰ) 求证: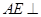 平面
平面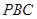 ;
;
(Ⅱ) 求证: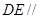 平面
平面 .
.