如图,已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
.
(Ⅰ)点 是直线
是直线 中点,证明
中点,证明 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
如图,三棱锥P ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点 
(1)若PA=2,求直线AE与PB所成角的余弦值;
(2)若PA ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC
如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4, ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE, =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2 ,
,
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
如图,三棱锥 中,
中, ,
,

(Ⅰ)求证: ;
;
(Ⅱ)若 ,
, 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正切值
所成角的正切值
如图,在等腰梯形 中,
中, 是梯形的高,
是梯形的高, ,
, ,现将梯形沿
,现将梯形沿 折起,使
折起,使 ,且
,且 ,得一简单组合体
,得一简单组合体 如图所示,已知
如图所示,已知 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,正三棱柱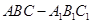 中,点
中,点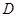 是
是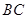 的中点.
的中点.
(Ⅰ)求证: 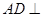 平面
平面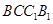 ;
;
(Ⅱ)求证: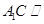 平面
平面 .
.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形, ,
,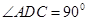 ,平面
,平面 底面
底面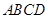 ,
, 为
为 中点,M是棱PC上的点,
中点,M是棱PC上的点,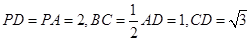 .
.
(1)若点M是棱PC的中点,求证: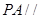 平面
平面 ;
;
(2)求证:平面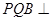 底面
底面 ;
;
(3)若二面角M-BQ-C为 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.