(本小题满分12分)已知四边形 为平行四边形,
为平行四边形, ,
, ,
, ,四边形
,四边形 为正方形,且平面
为正方形,且平面 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 为
为 中点,证明:在线段
中点,证明:在线段 上存在点
上存在点 ,使得
,使得 ∥平面
∥平面 ,并求出此时三棱锥
,并求出此时三棱锥 的体积.
的体积.
(本小题满分12分)如图,矩形 所在的平面与等边
所在的平面与等边 所在的平面垂直,
所在的平面垂直, ,
, 为
为 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
如图,已知四棱锥 中,
中, 平面
平面 ,底面
,底面 是正方形,
是正方形, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
在 中,
中, ,斜边
,斜边 .
. 以直线
以直线 为轴旋转得到
为轴旋转得到 ,且二面角
,且二面角 是直二面角,动点
是直二面角,动点 在斜边
在斜边 上.
上.
(1)求证:平面 平面
平面 ;
;
(2)当 时,求异面直线
时,求异面直线 与
与 所成角的正切值;
所成角的正切值;
(3)求 与平面
与平面 所成最大角的正切值.
所成最大角的正切值.
(本小题满分12分)如图,三棱台 中,
中, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 求证:平面
求证:平面 平面
平面 .
.
(本小题满分12分)如图,四棱锥P-ABCD中,底面 为菱形,且
为菱形,且 ,
, .
.
(Ⅰ)求证: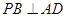 ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值。
的余弦值。
(本小题满分12分)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
(Ⅰ)求证:DE∥平面PAC.
(Ⅱ)求证:AB⊥PB;
(Ⅲ)若PC=BC,求二面角P—AB—C的大小.
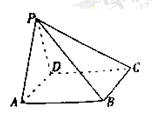
如图,已知三棱柱ABC—A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
(1)求证:PN⊥AM;
(2)若直线MB与平面PMN所成的角为θ,求sinθ的值.
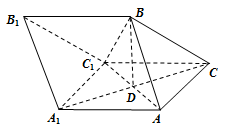
(本小题满分12分)如图,三棱柱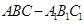 中,
中,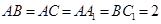 ,
,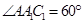 ,平面
,平面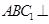 平面
平面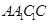 ,
,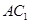 与
与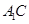 相交于点
相交于点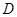 .
.
(Ⅰ)求证: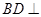 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知四棱锥P-ABCD,底面ABCD是 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
(Ⅰ)证明:DN//平面PMB;
(Ⅱ)证明:平面PMB 平面PAD;
平面PAD;
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,△PAD是正三角形,四边形ABCD是矩形,且 ,E为PB的中点.
,E为PB的中点.
(1)求证:PD∥平面ACE;
(2)求证:AC⊥PB
(本小题满分13分)在四棱锥 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求证: 平面
平面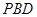 ;
;