如图, 为多面体,平面
为多面体,平面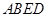 与平面
与平面 垂直,点
垂直,点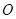 在线段
在线段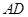 上,
上, △OAB,,△
△OAB,,△ ,△
,△ ,△
,△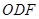 都是正三角形。
都是正三角形。
(Ⅰ)证明直线 ∥
∥ ;
;
(II)求棱锥F—OBED的体积。
如图,三棱柱中,侧面
为菱形,
.

(Ⅰ)证明:;
(Ⅱ)若,
,
,求二面角
的余弦值.
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
如图,四棱锥中,
为矩形,平面
平面
.

(1)求证:
(2)若问
为何值时,四棱锥
的体积最大?并求此时平面
与平面
夹角的余弦值.
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
如图(1),在三角形ABC中,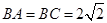 ,
,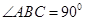 ,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.
,点O、M、N分别为线段的中点,将ABO和MNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.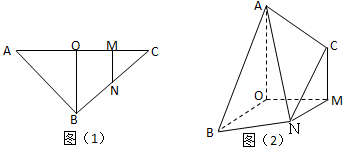
(1)求证: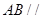 平面CMN;
平面CMN;
(2)求点M到平面CAN的距离.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
(1)求证:BC⊥A1D.
(2)求证:平面A1BC⊥平面A1BD.
(3)求三棱锥A1-BCD的体积.
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,
① 平面
平面 ;
;
② 平面
平面 ;
;
③CN与BM成 角;
角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。 (写出所有正确命题的序号)
(本小题满分12分)如图,在四棱锥P-ABCD中,PD^平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.

(Ⅰ)证明:PA∥平面BDE;
(Ⅱ)证明:AC^平面PBD.